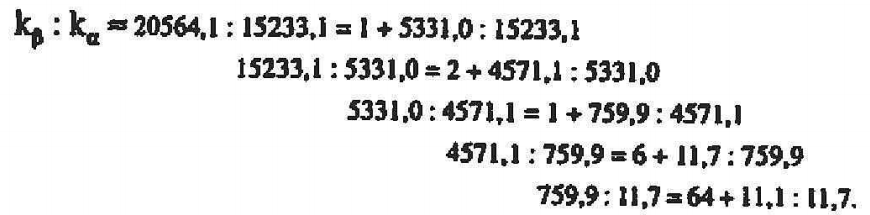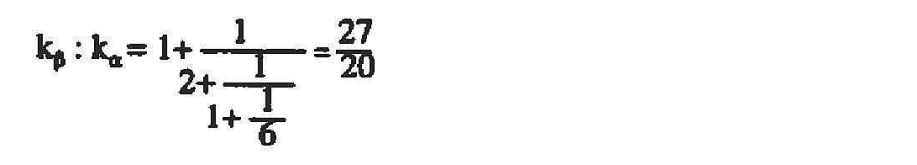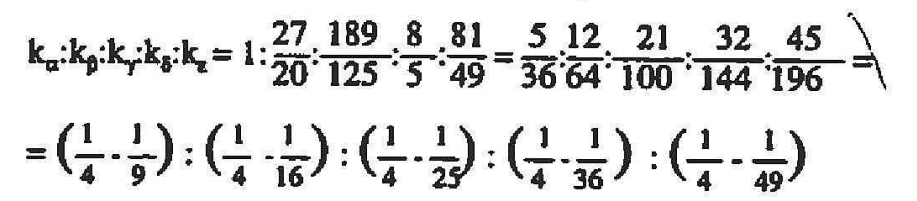Text:Rudolf Taschner – Der Blick in Gottes Karten

Rudolf Taschner – Der Blick in Gottes Karten

((1)) Aus einigen Passagen des Artikels von Ernst von Glasersfeld zieht der hellhörige Mathematiker Parallelen zwischen radikalem Konstruktivismus und formaler Mathematik:

((2)) Beide gründen auf einer fundamentalen Ablehnung: Der radikale Konstruktivismus lehnt den Begriff der ontischen Wahrheit ab ((57)). Die formale Mathematik verwirft die Forderung, Axiome haben evident zu sein.

((3)) Beide entwerfen eine gleichsam „systemimmanente“ Rechtfertigung des von ihnen gebilligten Denkens: Der radikale Konstruktivismus ersetzt Wahrheit durch Viabilität, womit die Forderung gemeint ist, Aussagen haben einerseits in bezug auf bereits getroffene Aussagen und andererseits in bezug auf die vom denkenden Subjekt als „Tatsachen“ benannte Erfahrungen angepaßt zu sein ((27)). Die formale Mathematik ersetzt die Evidenz von Axiomen durch die Forderung der Vollständigkeit, Widerspruchsfreiheit und Unabhängigkeit eines Axiomensystems und demgemäß ersetzt sie Wahrheit durch Ableitbarkeit aus den Axiomen gemäß eines formalen Kalküls.

((4)) Beide erfreuen sich totaler Immunität: Der Skeptiker des radikalen Konstruktivismus gilt, sobald er mit den strengen Regeln der „Grammatik“ dieses Denksystems bricht, als heillos verwirrter Metaphysiker ((20)). In der formalen Mathematik ist die Lage ähnlich: Hilbert, der Ahnherr der formalen Mathematik, hat dieses in sich geschlossene und daher von außen unangreifbare System deshalb geschaffen, damit ihn niemand aus dem von Cantors Mengenlehre geschaffenen „Paradies“ hinauswerfen könne. Tatsächlich hielt Poincarä Cantors Mengenlehre für eine „Krankheit“ und empfand demgemäß das von Hilbert aus seiner Innensicht Paradies genannte System eher als eine unheilvolle Falle, in die Hilbert und mit ihm alle anderen formalen Mathematiker getappt sind. Bekanntlich verschärfte sich der mathematische Grundlagenstreit im dritten Jahrzehnt dieses Jahrhunderts ohne entschieden worden zu sein: Gegen ein immunes System zu kämpfen, wie es die formale Mathematik ist, erwies sich letztlich als sinnlos.

((5)) Beide gebärden sich im Unterschied zu „fundamentalistischen“ Ideologien wie Marxismus, Darwinismus oder Psychoanalyse als tolerant - wenn auch mit dem Anflug einer gewissen Herablassung: Der radikale Konstruktivismus leugnet keineswegs ontische Realität, er hat ja nicht einmal die Veranlassung, dies zu tun, weil er jedes sinnvolle Sprechen darüber für obsolet erklärt ((58)). Die formale Mathematik leugnet keineswegs die Anwendbarkeit der Mathematik (ihre Vertreter würden sich sogar eher die Zunge abschneiden, als dieszu tun, weil allein in der Nützlichkeit der Mathematik ihr Prestige und damit ihre gesellschaftliche Förderung politisch argumentierbar ist), obwohl aus dem System der formalen Mathematik unverständlich bleibt, warum Mathematik so flexibel anwendbar ist, ja was „Anwendung“ letztlich überhaupt bedeutet.

((6)) Beide sind - ebenfalls im Gegensatz zu „fundamentalistischen“ Ideologien - frei vom unbedingten Anspruch auf Wahrheit: Der radikale Konstruktivismus deshalb, weil ihm der Begriff der „Wahrheit“ als solcher prinzipiell suspekt ist Die Ausführungen von Ernst von Glasersfeld über die „Quellgebiete“ seines Denkens verstehe ich dementsprechend als Bekundung für die Plausibilität, nicht aber als Beweis für die unbezweifelbare Gültigkeit des radikalen Konstruktivismus. Genauso ist der formalen Mathematik der Gedanke, man könne ihre Gültigkeit stringent herleiten, völlig fremd: ihr genügte die Absicherung bezüglich Vollständigkeit und Widerspruchsfreiheit (selbst diese ist nach den Sätzen Gödels nicht zu erreichen) - daß damit die Vorstellung von absoluter Wahrheit verbunden sei, ist jedoch völlig abwegig.

((7)) Beide Systeme schließlich - und dies begründet meine Skepsis, die ich gegen beide Systeme hege, - verkennen die Stichhaltigkeit von Argumenten, die mit unvermittelter Anschauung, Evidenz oder Intuition einhergehen. Denn in der formalen Mathematik haben die Aussagen allein auf dem Sprachspiel zu beruhen, das auf der Grammatik des Axiomensystems und der Ableitungsregeln gründet. Und im radikalen Konstruktivismus sind Aussagen in das Netz der bereits als viabel betrachteten Aussagen einzubinden und somit letztlich nur von diesem Aussagennetz abhängig (dessen einzelne Knoten - angepaßt auf eben erfahrene „Tatsachen“, was immer man unter „Tatsache“ versteht, - stets ausgebessert werden dürfen).

((8)) Damit wird auf zu viel verzichtet. Der formalen Mathematik gelingt es zum Beispiel nicht, mit ihrer Beschreibung des Systems der reellen Zahlen den intuitiven Begriff des Kontinuums stimmig zu fassen - der für mich zwingendste Grund dafür, Mathematik nicht formal zu konstituieren.

((9)) Daß sich auch der radikale Konstruktivismus durch den Verzicht auf ontische Wahrheit und das Leugnen ihres Aufleuchtens in den Sternstunden des auf seine Intuition vertrauenden Forschers zu viel vergibt, sei exemplarisch an einer (seltsamer Weise kaum allgemein bekannten) Begebenheit erläutert, die sich entscheidend für die Entdeckung der Quantentheorie erweisen sollte: 1814 entdeckte der Optiker Joseph Fraunhofer die nach ihm benannten Absorptionslinien im Sonnenspektrum. 1859 erkannten der Chemiker Robert Wilhelm Bimsen und der Physiker Gustav Robert Kirchhoff, daß die Spektrallinien Fraunhofers für jedes chemische Element kennzeichnende Wellenzahlen (d.h. Anzahlen von Lichtwellen pro Zentimeter) aufweisen, was die beiden unter anderem zur Entdeckung der Elemente Cäsium und Rubidium führte. Die Wellenzahlen des leichtesten und ersten Elements im Periodensystem, des Wasserstoffs, im sichtbaren Licht lauten zum Beispiel kα = 15233,1/cm, kβ = 20564,1/cm, kγ = 23032,4/cm, kδ = 24372,9/ cm, kε = 25181,3/cm. Obwohl es sich hierbei um beeindruckend genaue optische Messungen handelt (das Ungefähr-gleich-Zeichen = erinnert daran, daß man dennoch mit Meßunschärfen zu rechnen hat), blieb für lange Zeit völlig unklar, warum (d.h. in der Sprache der Physik: nach welchem mathematischen Gesetz) die mit α, ß, γ, δ, ε numerierten Spektrallinien des Wasserstoffs gerade diese Wellenzahlen besitzen. 1885 fand der Schreib- und Rechenlehrer Johann Jakob Balmer das Gesetz. Bemerkenswert ist, wie Balmer es entdeckte, da zu seiner Zeit alle Versuche, anhand eines Modells den Wellenzahlen auf die Spur zu kommen, kläglich versagten. Balmer ging allein von den fünf oben angegebenen Daten aus und unterwarf sie der bereits aus der antiken griechischen Mathematik bekannten Methode der Kettendivision: Die größere zweier Wellenzahlen wird durch die kleinere dividiert, danach wird der Divisor durch den eben erhaltenen Rest dividiert und so weiter. Wir greifen die Wellenzahlen kα und kβ als Beispiele heraus; hier lautet diese Kettendivision;

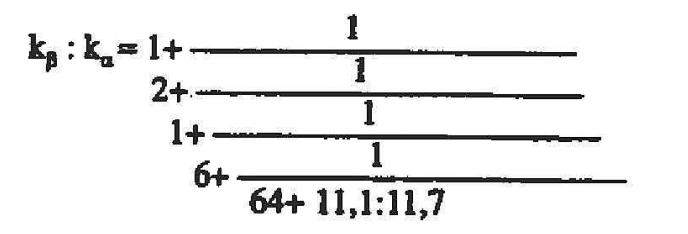
Für das Verhältnis kβ : kα selbst ergibt sich hieraus:

Der brillante Gedanke Balmers war, daß der zuletzt berechnete, unverhältnismäßig große Nenner 64 + 11,1 : 11,7 = 65 bereits unterhalb der Meßgenauigkeit rangiert - er könnte innerhalb der Meßtoleranz genauso gut durch unendlich ersetzt werden. Diese Ersetzung nimmt Balmer vor. Er vertraut darauf, daß der wahre Wert des Verhältnisses

beträgt. Dieser Bruch mit relativ kleinen Zähler und Nenner beschreibt einerseits das gemessene Verhältnis hinreichend genau und steht andererseits für die Zuversicht Balmers, daß die Gesetze der Natur im Grunde einfach sind. Mit derselben Methode gewinnt Balmer die - seiner Meinung nach exakten - Verhältnisse kγ : kα = 189 : 125, kδ : kα = 8 : 5, kε : kα = 81 : 49 und erhält so aus der fortlaufenden Proportion

die nach ihm benannte Spektralformel.

((10)) Für die Diskussion des radikalen Konstruktivismus ist an diesem Beispiel entscheidend: Die Herleitung dieses Gesetzes erfolgte direkt von den Daten zu den (von Balmer als exakt vermuteten) Zahlen. Balmer benützte weder eine Theorie noch ein die Natur simulierendes Modell - er konnte dies gar nicht, denn das erste Modell, welches die Serienformel Balmers aus einem Atommodell „erklärte“, wurde mehr als 25 Jahre später von Niels Bohr entworfen.

((11)) Es ist ferner bemerkenswert, daß die in der „Kopenhagener Deutung der Quantentheorie“ erstellte Verfeinerung des Bohrschen Modells überdies gestattet, die Breite der Spektrallinien des Wasserstoffs zu verstehen: aus dieser Sicht bedeutet Balmers Vertrauen in die Verhältnisse mit kleinen Zählern und Nennern die Annahme eines idealen Wasserstoffatoms, eines von allen äußeren Einflüssen unabhängigen quantentheoretischen Zweikörperproblems. Wäre diese Idealisierung in der Natur verwirklicht, reduzierten sich die Spektrallinien tatsächlich auf mathematisch exakte Linien an den von Balmer genau vorhergesagten Stellen im Spektrum - allerdings mit dem Nachteil, daß man sie nicht messen könnte, denn die mathematisch exakte „unendlich dünne“ Linie würde im Spektrum unsichtbar bleiben.

((12)) So gesehen bestätigt sich an diesem Beispiel erneut die von Ernst von Glasersfeld zitierte Erkenntnis des Xenophanes, daß es Balmer letztlich doch nicht erlaubt war, sich die Welt - und sei es auch nur die Welt des realen Wasserstoffatoms - so vorzustellen, wie sie „wirklich“ ist. Die Natur entzieht sich letztlich immer den Zugriffen des sie ertappen wollenden Forschers.

((13)) Das Beispiel der Entdeckung von Balmers Formel belegt jedoch, daß man nicht vor die Alternative gestellt ist, sich entweder für den Anspruch des naiven Beobachters, er besitze eine in allen Details stimmige Vorstellung von der Natur, oder aber für die radikale Ablehnung des Konstruktivisten, von einer Welt jenseits unserer Sinne und Begriffe überhaupt zu sprechen, zu entscheiden. Wird der Anspruch des naiven Beobachters zurecht bereits von den griechischen Denkern verworfen, mißachtet die Ablehnung des Konstruktivisten ebenso sträflich die Kraft der Intuition des genialen Forschers. Nur durch sie wird Naturwissenschaft erst interessant, ohne sie bleibt unverständlich, wie Naturwissenschaft überhaupt zustande kam.

((14)) Einstein spricht in dem Zitat ((8)) zurecht von der unüberbrückbaren Differenz zwischen den Modellen der Physiker und der Wirklichkeit. Er spricht aber an anderer Stelle auch vom Reiz der Physik, daß sie erlaubt, „dem heben Gott in die Karten zu schauen“. Balmer war zum Beispiel ein „Blick in Gottes Karten“ gegönnt, als er von den Meßresultaten auf die „exakten“ Werte schloß. Eine Wissenstheorie, die dies nicht zu würdigen versteht, geht daher am zentralen Kern von Erkenntnis vorbei.