Subitizing: The Role of Figural Patterns in the Development of Numerical Concepts
| Subitizing: The Role of Figural Patterns in the Development of Numerical Concepts | |
|---|---|
| Title | Subitizing: The Role of Figural Patterns in the Development of Numerical Concepts |
| Author | Ernst von Glasersfeld |
| Date of Publication | 1982 |
| Published in | Archives de Psychologie |
| Location | Genf |
Glasersfeld E. von (1982) Subitizing: The Role of Figural Patterns in the Development of Numerical Concepts. Archives de Psychologie 50: 191–218. Available at http://vonglasersfeld.com/cgi-bin/index.cgi?browse=journal
This paper was downloaded from the Ernst von Glasersfeld Homepage, maintained by Alexander Riegler. It is licensed under a Creative Commons Attribution-NonCommercialNoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/ or send a letter to Creative Commons, 559 Nathan Abbott Way, Stanford, CA 94305, USA.
The Role of Figural Patterns in the Development of Numerical Concepts[1]
No thinking, not even the Purest, can take place but with the aid of the universal forms of our sensua1ity; only in them can we comprehend it and, as it were, hold fast. – Wilhelm von Humboldt, 1796.[2]
Whenever we hear a number word, we know, as Euclid already knew, that it refers to a conceptual unit that is itself composed of units. Under normal, everyday circumstances there is no problem about the component units. We know what they are, because we are told by the speaker, or we can see them in front of us, or we can recall them from some specific experiental situation. That is to say, under ordinary circumstances number words are used with reference to actual or represented (imagined) perceptual items. In mathematics, however, that is not the case, even if, as in this paper, we consider nothing but whole numbers and leave aside all the fancier items which mathematicians have come to call “numbers”. Thus, when children are taught arithmetic they are expected to “abstract” the meaning of number words from the perceptual situations in which we ordinarily use them. They are asked to figure out what, for instance, 7 + 5 is, and – though at first they may he given a crutch in the form of tangible beads, checkers, or cookies – they are supposed to solve that kind of problem eventually without the help of any perceptual or representational material. Even if that expectation is fulfilled by many children, the fact that some fulfill it slowly and others not at all, raises the question of how one could specify more precisely what it is that has to be done.
Two earlier papers from our research group dealt with some aspects of that question. The first presented an analysis of counting types that explicated the development of the ability to count abstract unit items that may have been derived from, but are no longer dependent on, sensorimotor material (Steffe, Richards, & von Glasersfeld, 1979), the second a theoretical model for the abstract conceptual structures called “unit” and “number” (von Glasersfeld, 1981 a).
In the pages that follow I shall focus on the phenomenon of “subitizing” which has been known a long time but was usually treated as an oddity that is at best marginal in the acquisition of numerical skills.[3] Steffe’s large-scale investigations of children’s progress towards arithmetic competence, however, strongly suggest that perceptual recognition and subsequent representation of small lots up to four or five elements play an indispensable role in the development of arithmetic operations (Steffe, von Glasersfeld, Richards & Cobb, in prep.).[4] The lines of thought I am here pursuing all spring from that interpretation of children’s behavior in their attempts to solve simple number problems and, in particular, from Steffe’s suggestion that they use “subitizing” in a representational mode when no perceptual items are available. I shall argue, however, that perception of composite figural patterns plays an even more fundamental role as an essential building block in the genesis of the concept of number. In order to substantiate this claim, I shall begin by presenting a model developed earlier in the context of psycholinguistic investigations and intended to explicate the connection between words and their meaning. I shall then apply that model to the special case of number words that become associated with spatial as well as temporal configurations of perceptual items. Finally, I shall try to show how the model, in conjunction with Piaget’s notion of “empirical” (or “generalizing”) and “reflective” abstraction, enables us to integrate the perceptual recognition of small lots (i.e. “subitizing”) into a more general theory of numerical concepts and operations.
Words and meanings
Number words, like other words and conventional means of communication, are embedded in the general semiotic system of the human species which we have all learned to use by growing into it rather than by conceptualizing the way in which it works. The apparent effortlessness with which, as a rule, we acquire language and become more or less proficient communicators without ever becoming aware of how language functions – indeed, the very conception of natural language – has helped to maintain some ingenuous “common sense” notions which, for a long time precluded any detailed understanding of the processes involved. For instance, the idea that words could refer to objects in a user-independent “real” world has been as much of a hindrance to the study of language as the purported link between number words and quantities of objects has been for an understanding of numerical operations.
Much time and futile struggle could have been saved if more attention had been paid to what Ferdinand de Saussure taught about language at the beginning of this century.[5]
“It [language] is a system of signs in which the only essential thing is the union of meanings and sound-images, and in which both parts of the sign are psychological” (de Saussure, 1959, p. 15).
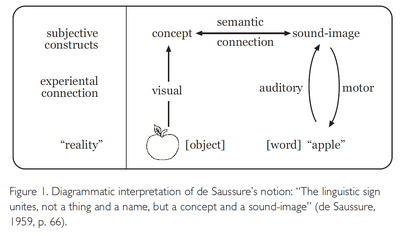
“The linguistic sign unites, not a thing and a name, but a concept and a soundimage” (ibid., p. 66).
What de Saussure said can be complemented by a simple diagram that shows that the “semantic connection” is always on the experiencer’s side of the experiential interface and not in what is often called the “objective environment” (see Fig. 1). De Saussure’s term “sound-image” refers to conceptual representations abstracted from the experience of spoken words and is, thus, analogous to “concept” which refers to conceptual representations of non-verbal experiences. Reality and the items considered part of it, are put between quotation marks because, from the constructivist perspective, they are an observer’s externalized percepts rather than “real” things or events in an observer-independent ontological world (cf. von Glasersfeld, 1974; Richards & von Glasersfeld, 1979).
In their classic work The Meaning of Meaning, Ogden and Richards (1946) drastically simplified that arrangement by compounding (and thus confounding) “concept” and “sound-image “at the apex of a triangle whose lower corners pointed at “referent” (object) and “symbol” (word) respectively. Strongly influenced by the rise of behaviorism they apparently were uneasy about “mental” constructs such as concepts and sound-images but they still felt the need to put the word “thought” at the apex of their triangle and it is certainly to their credit that they emphasized the fact that the direct connection between symbol and objective referent is an imagined or “purported” one. However, their simplification was an unfortunate step in the direction of radical Behaviorism, the school that later flourished and tried to eliminate thought altogether and to substitute a directly connected “stimulus” and “response” for symbols and referents. It has taken a long time to overcome this categorical elimination of mental operations and meaning, both in linguistics and in psychology. But now the general attitude has changed and we may once more adopt the view held at the beginning of the century when not only de Saussure but also Charles Peirce had realized that symbols and their referents could have no connection other than that formed in the minds of symbol users.
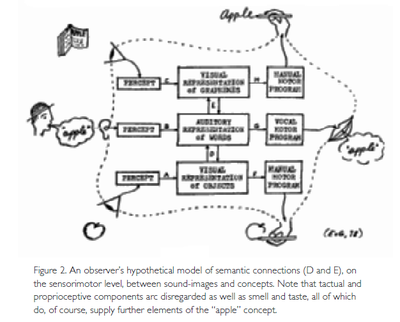
Rather than simplify the schematic arrangement of de Saussure’s “psychological” connection between words and things we must amplify it considerably before we can adopt it as plausible model of the human word processor. For the present purpose it will suffice to say that such a model must include the step from percepts to representations and the step from representations to motor programs for the production of utterances (see Fig. 2).[6]
This break-down discriminates between hearing a word and speaking a word, and it shows the dual semantic connections of auditory word-representations with visual representations of perceptual objects on the one hand, and on the other, with representations of written (or printed) words. The diagram is grossly simplified in that it illustrates only the figural, sensorimotor level of the linguistic skills. The operative, or conceptual, levels would have to be added above it, in a third dimension. It does not show general, more or less “ideal” concepts such as “circularity” or “sphericality” – i.e. constructs that play an important role in the recognition (assimilation) of perceptual patterns (e.g. apples) but are themselves not parts of, but results of prior sensory experience. Abstractions, as von Humboldt said with exemplary clarity, arise from a process that has generally been called “reflection”:
“The essence of thinking consists in reflecting, i.e., in distinguishing the thinking from that which is thought about” (von Humboldt, translation by Rotenstreich, 1974, p. 211).
The same process has been described and analyzed by Husserl in 1890[7] and Piaget has used the term “reflective abstraction” all along, distinguishing it from “empirical abstraction”. Recently (Piaget, 1975, p. 63) he has come to the conclusion that the two types of abstraction take place in constant interaction. For the purpose of explication, however, it is helpful to present the two levels of abstraction sequentially, even if in the child’s actual development there is, as Piaget now says, frequent reciprocal interaction between them.
In the context of this paper I shall use “empirical abstraction” to characterize the abstracting of figural patterns from sensorimotor |experience, whereas I shall use “reflective abstraction” to indicate a further level of abstraction that uses the results of empirical abstraction and other operations as raw material. Thus I shall maintain that it is empirical abstraction when the experiencing subject attends, not to the specific sensory content of experience, but to the operations that combine perceptual and proprioceptive elements into more or less stable patterns. These patterns are constituted by motion, either physical or attentional, forming “scan-paths” that link particles of sensory experience. To be actualized in perception or representation, the patterns need sensory material of some kind, but it is the motion, not the specific sensory material used, that determines the patterns’ character. Because of this dependence on some (unspecified) sensory material and motion, they are called figural patterns. Reflective abstraction, on the other hand, takes place when the experiencing subject attends only to the mental operations and abstracts them from whatever sensorimotor context that may have given rise to them. Numerical concepts, as Piaget and Szeminska (1967; Piaget, 1970) and many others have pointed out, are stripped of all sensorimotor properties and, therefore, necessarily involve reflective abstraction.
A way to obtain wholly abstract numerical concepts that are independent not only of sensorimotor material but also of figural patterns, was proposed in an earlier paper (von Glasersfeld, 1981a). Here I want to turn to the question of how the more primitive, perceptual concepts (that precede the conception of number) fit into the general semiotic system I have sketched out above and, especially, how their links to number words develop.
Number words without numbers
Number words are words and, as happens with other words, children can learn to say them long before they have formed perceptual representations, let alone abstract concepts to associate with them (in Fig. 2, this corresponds to establishing the straight connections B and G prior to the connections D and E). The learning of empty, as yet meaningless words is easier and more likely when the words have a fixed order in which they frequently occur. That is, of course, the case with number words as well as with the rhymes and prayers which children can learn without the least understanding. Piaget remarked long ago that the reciting of the initial string of number words is usually imposed on children at a very early stage (i.e. before they are four years old) but is then “entirely verbal and without operational significance” (Piaget & Szeminska, 1967, p. 48; cf. also Pollio &: Whitacre, 1970 Potter & Levy, 1968; Saxe, 1979).
At an even earlier age, however, children may learn a few isolated number words in the same way in which they learn object-words. It usually happens with the first number words of the conventional sequence, at least from “one” through “five”; and since those are the very ones that are then used in subitizing, we have to ask how words of any kind are initially acquired.
A twelve-month-old may come to associate the auditory experience of the word “spoon” (recurrently uttered by mother) with the global sensorimotor experience of being spoon-fed or trying to feed himself. He may then attempt to reproduce the auditory experience through vocal act of his own. By the age of 24 months, at any rate, the child will have segmented and organized his or her sensorimotor experience quite sufficiently to recognize the spoon in the visual field alone (without tactual or motor complements) and from any angle. Indeed, the spoon will have become a “permanent object” (Piaget, 1937) with characteristic visual pattern and other sensorimotor aspects that can be called up as a representation when the object is not in sight, and that representation will have a firm semantic connection with the sounde-image of the word “spoon” (connection D in Fig. 2).
Once semantic connections are beginning to be formed, any recurrent figural pattern can be semantically associated with a number word. That children actually do this, has been observed quite frequently (e.g. Wirtz,1980,p.2).
Figural patterns can be divided into two groups: Those that are constituted as a spatial configuration (to which corresponds a scan-path) and those that are constituted as temporal sequence (to which corresponds a rhythm). In both groups empirical abstraction from the actual sensory material out of which particular configurations or sequences are built up, yields figural patterns that have a certain general applicability and can be semantically associated with specific names. Thus we have, for instance, the notion of “triangularity” that enables us to see spatial configurations as triangles irrespective of their color, size, angles, or other sensory properties; and in the temporal group we have notions such as “waltz” or “iambus” which enable us to recognize these specific rhythms irrespective of the auditory particulars with which they happen to be implemented. Since subitizing has mostly been studied as a visual phenomenon, I shall first deal with the semantic connections formed between number words and spatial configurations and only then with those involving temporal patterns.
If a child is given a set of wooden or plastic numerals to play with and these toys are occasionally pointed out by the parents as a “three”, a “one”, an “eight”, etc., the child will quickly associate the visual patterns with the appropriate name. If he then gets dominoes, he will add dot-configurations as alternative semantic connections to the number words, and he will do the same for the characteristic arrangements of design elements on playing cards as soon as he is introduced to a card game. In fact, the child will continue to add connections for any pattern that experientially co-occurs consistently with one and the same number word. That is in no way different from what a child has to do, and does, to acquire proficiency in the use of ordinary words such as “dog”. If a poodle happens to be part of the household, a representation of the poodle-percept will be the first meaning of the word. As other dogs enter the child’s experience, new perceptual patterns will be associated with the word. Though there have been theories that suggested it (e.g. Katz & Foder, 1963), it is utterly inconceivable that a child actually forms a universal representation of dog percepts when he or she discovers that adults use the word “dog” to refer, not only to his poodle, but also to a Dachshund, a Great Dane, a St. Bernard, and a bulldog. No common figural representation could cover that variety of canines without erroneously including members of other species as well (cf. Barrett, 1978). Hence children may over-extend the use of the word and say “dog” when first they see a lamb or a calf. But children do learn to use the word “dog” appropriately for visually quite different animals that belong to the class of canines only because zoologists have adopted a taxonomic definition that is based on features which are remote from children’s visual or sensorirnotor experience. The acquisition of appropriate use becomes plausible if we think of it as the result of alternative representations linked to one word by separate associations rather than as a variety of experiences connected to one common representation.[8]
The hypothesis of alternative figural representations that are “equivalent” in that they are all semantically connected to one word, has the virtue that it at once fits how children come to recognize a considerable variety of figural patterns as legitimate referents of a number word long before they have any conception of number or numerosity. The sound image of “three” is easily associated with whatever perceptual configurations are explicitly called “three” by the adults in whose company the child grows up. There will be finger patterns, patterns of dots and lines, arrangements of particular design elements (hearts, diamonds, etc.), and of course the variations of the numeral 3.
Some of these figural patterns area “iconic” in that they are composites of perceptual units which, if considered quantitatively (by a counter who already has numerical concepts) represent the numerosity designated by the number word with which they are associated. Others, like the Arabic numerals (and the Roman numerals above III) are not iconic, because they are not constituted by a collection of items that has the indicated numerosity. Thus I am suggesting that, in subitizing, the child associates figural patterns with number words by a semantic connection and not because of the number of perceptual units of which they are composed. In acts of subitizing, the figural patterns that give rise to it are taken as figural wholes and not as composites of units. In fact, they are recognized as a global configuration, not as a collection of countable items. Perhaps the most convincing demonstration of the fact that subitizing does not involve any perception of number or numerosity is the card player’s ability to recognize and name playing cards even when only part of the individual perceptual units that constitute the configuration are visually accessible to him (see Fig 3). The names of the cards are, of course, number words.
In this case however, the number words are not evoked by perceived numerosities but rather by configurations familiar enough to be representationally completed from partial perceptions. This recognition is a striking manifestation of a capability the Gestalt psychologists observed long ago. Piaget and Szeminska characterized it well when they said that, for instance, the corner points of a triangle correspond to the corner points of other triangles, irrespective of the knowledge that their number is the same – just as the parts of one human face correspond to those another (1967, p. 93). The corner points of one triangle “correspond” to those of all triangles because they are turning points in a scan-path that is in that respect the same for all triangles regardless of their particular angles or size.[9] Similarly, the parts of one face correspond to the parts of all faces because the same scan-path fits them all (except some painted by Picasso, which indeed require a non-standard recognition procedure). A common scan-path, namely a straight one, also correlates all figural arrangements of two items; and many arrangements of four items can be perceived by a quadrilateral path. Since such characteristic paths can be abstracted as figural representations of “twos”, triangular “threes”, quadrilateral “fours”, and certain “fives”, they reduce the number of individual figural representations that have to be remembered in the case of spatial patterns consisting of up to five perceptual units. And this economy is achieved without any reference to number, nor is the concept of numerosity involved in the procedure (cf. Mandler & Shebo, 1980).
When I said earlier that the alternative figural representations associated with one and the same number-name are “equivalent”, I was referring to their semantic equivalence. The ease or immediacy with which the individual configurations are visually recognized may, of course, vary greatly. Familiarity as well as structural characteristics of the patterns influence both speed and accuracy of recognition. The work of Brownell, who undertook a monumental study of the “apprehension of visual concrete number” (1928), contains many observations that indicate children’s preferential association of specific configurations with certain numbers and that the fact that figural regularities facilitate the “apprehension” of the correct numerosity. Unfortunately Brownell started from the realist assumption that numbers are “concrete” and can therefore be perceptually “apprehended”. Hence he assumed that, no matter how, say, four elements were arranged in space, the perception of their number would always be the same task, and he took great care to average the measurements obtained with different “sensory material”. Indeed, he criticized the earlier study by Howell (1914) because it used only one type of “number pictures”, namely the quadratic type, which represents numbers by placing dots in the corners of imaginary squares. From my point of view, however, Howell’s study yields results that are important even if they are precisely what we would intuitively predict. His data show that the numbers represented by the full quadratic pattern, or by multiples of it, are relatively easier to “apprehend” than the ones with patterns that contain half quadrats, and that these in turn, are relatively easier than the others that contain a separate, single dot. Perceptually this makes good sense, and it is precisely what we would expect, once we conceive the problem as a visual one of pattern recognition whose only connection with numbers is that specific number words (and through them, at the level of adult operating, numerosities) have been semantically associated with specific dot patterns.
Howell’s study, of course, shows the “easy pattern effect” only for the quadratic arrangement of four dots in one orientation (as though they were in a horizontal-vertical grid). It is possible – and some of Brownell’s data seem to suggest it – that the “square four” is even easier to recognizes when it is presented obliquely as a “diamond”. Similarly, we would guess that the domino pattern of five is more familiar than a square four with a fifth dot beside it.[10] But these are questions in the area of visual pattern recognition. In the context of children’s subitizing, these patterns have no connection with the concepts of number or numerosity.
Temporal patterns
There are dot patterns and other spatial configurations that are obviously not distinguishable on the basis of qualitative motor characteristics of scan-paths. If two dots are recognized as a characteristic configuration by the sole fact that they are connected by a straight scan-path, then three, four, or more dots in linear arrangement would be considered the same. Yet this is not the case. Starkey and Cooper (1980) have elegantly shown that even infants of less than six months discriminate quite reliably three dots in a line from two, whereas they do not seem to discriminate between four and six. We may safely assume that infants of that age cannot count. On the other hand, the experiment made clear that the discrimination does not depend on the distance between the dots or on the over-all extension of the display. Hence there must be some inherent difference in the process of perceiving two as opposed to three dots.[11] That difference, I suggest, arises from the capability of the nervous system to differentiate between the temporal patterns constituted by a succession of two perceptual acts as opposed to one or three. “Perceptual act” in this context means no less and no more than the isolation of any item whatever from the rest of the experiential field which, in the case at hand, can be reduced to the visual field. In other words, I am positing a neural mechanism that distinguishes a dual incidence of a given event from a single or a treble incidence (von Glasersfeld, 1981b). What will be considered a dual event, rather than two single ones in succession, depends of course on temporal parameters which we must assume to be inherent in the system – an assumption that can not be invalidated by the observation that these temporal parameters can, under certain circumstances, be modified by experience, practice, or training.
The best-known instances of non-numerical discrimination and recognition of single, dual, treble, etc., events are probably those that occur when we listen to music, where they form the experiential material that goes by the name of “rhythm”. Recent work with children leaves no doubt that the ability to remember, recognize, and replicate simple rhythms (by clapping or tapping) is manifested prior to any abstract or notational representations of such rhythms (Bamberger, 1975, 1980, 1982). That is to say, a sequence of beats which an adult might capture in a conventional notation, is recognized by the child as a figural pattern in a way analogous to that in which visual shapes are first recognized, but with the difference that the rhythm is a configuration in time, whereas the shapes appear as configurations in space (von Glasersfeld, 1979b). From my point of view, it is particularly interesting that the children in that study had little or no difficulty in “drawing” the rhythms by inventing their own visual representations.
This readiness to translate a temporal pattern into a linear spatial one strongly supports my assumption that the visual perception of a linear arrangement of items can, indeed, be characterized (and distinguished from other visual experiences of the kind) by its rhythmic properties. In both vision and audition the temporal pattern is constituted by a sequence of perceptual acts which are given their structure by a succession of attentional pulses. This is rather obvious in auditory experience, which is necessarily perceived as an ordered sequence of events in time. In visual experience the sequentially is obscured because, under most circumstances, the individual perceptual acts that constitute a spatial configuration are not subject to an obligatory order.[12] That is why linear arrangements are something of a special case: There, a definite order is at least strongly suggested by the ease and economy of the linear scan-path.
A striking example of the ability to transpose spatial into temporal patterns is the telegraphist’s translation of written Morse code into a sequence of motor acts that make and break an electric contact. Here the conventional order of the left to-right line is turned into a temporal order. The groups of dots and dashes on the source tape are neither counted nor perceived as numerical structures – they are taken as patterns of perceptual acts that can be immediately realized in terms of motor acts because the rhythmic configuration remains experientially the same in both modes.
In short, then, I am suggesting that the infants’ ability to distinguish between linear displays of one, two, and three dots (Starkey & Cooper, 1980), young children ‘s facility for depicting auditory patterns graphically (Bamberger, 1975), the telegraphist’s skill of translating visual into motor sequences, and, finally, the general ability to subitize linear arrangements of perceptual items, can all be reduced to an underlying capacity to distinguish, recognize, and represent simple temporal configurations that have a characteristic iterative structure. Such iterative structures have rhythmic patterns that can be empirically abstracted as figural patterns from sensory events, not only in the auditory mode, but also in the kinesthetic, tactual, and visual modes, because, in all these modes of experience, structure is constituted by a patterned succession of attentional moments that was experientially determined by the sequence of sensory signals. Once abstracted, these rhythmic patterns may be semantically associated with number-words. The link to a number word, however, does not turn them into numerical concepts. Conceptually they are still figural patterns. Only “reflective” abstraction – the focusing of attention on their iterative structure rather than on the actual or representational sensory material with which that structure happens to have been implemented – can raise them to the level of “pure” abstraction that is characteristic of the conception of numbers (von Glasersfeld, 1981a).
On the other hand, already as figural patterns consisting of sequences of perceptual items, representations of such rhythmic structures make possible the recognition of specific sequential configurations of dots, checkers, fingers, etc., as instances of patterns that are associated with one of the number-words between one and five. Thus, analogous to the way in which a characteristic scan-path serves as the criterial recognition feature for specific classes of spatial patterns (e.g. triangles), a characteristic rhythmic structure serves as the criterial recognition feature for large classes of sensory events which, experientially, can be reduced to temporal patterns. Since these classes comprise not only auditory and motor events (whose nature is sequential in any case), but also visual and tactual events whose sequentiality is created by a relatively fixed linear order of the perceptual process, the recognition of rhythmic structures plays an important role in the phenomenon of subitizing and as a necessary precondition to the reflective abstraction of numerical concepts from linear configurations of items such as dots and tiles, and from Finger patterns.
The problem of numerosity
Number and numerosity, thus, do have a root in the processing of percepts and hence there arises the question of how that involvement comes about. I am proposing the thesis that there are several experientially independent paths that contribute to the generation of the complex conceptual structure that we, as adults, ordinarily call number. All three paths contribute to the adult concept, but none of them entails the pursuit of the others.
Before attempting to delineate these paths, let me justify the emphasis on the complexity of the number concept. In an earlier paper (1981a) I presented an attentional model for the structure of number concepts and concentrated on the material out of which such concepts may be formed, namely attentional pulses. I explicitly stated that although the products of the attentional construction have numerosity, their structure must not be confused with the concept of numerosity. That distinction is particularly important because, ordinarily, when we use the word “number” we do not specify whether we are speaking of a numerical structure or of its numerosity. The difference may become more palpable if we compare it to a logically analogous difference in another area. The colors we perceive can be correlated to the frequency of waves which we postulate as the structure of light. If we then say yellow lies between such and such frequencies, we are talking about the structure of yellow, not about the characteristic quality of yellowness that we distinguish from orange and green. Although we can correlate wave lengths and frequencies with our experience of color, they tell us nothing about that experience, nor why it should change as we move along the frequency scale, why we see blue as we move up from green, and red as we move down from orange. Similarly, the attentional model provides a way of thinking about the structure of number concepts but, by itself, it tells us nothing about what we call “quantity” or “numerosity”.
Unlike the color analogy, where there is, at present, no way at all of relating the qualitative experience to any structural model, I shall suggest in what follows how the conception of numerosity can be related to the attentional model of number. I have stressed the complexity of number concepts because, in the view presented here, they comprise, on the one hand, an attentional structure that characterizes all of them – analogous to the wave notion that characterizes the structure of all colors – and, on the other hand, a conception of numerosity that is itself a composite of the products of several relatively independent conceptual developments.
Experiencing units of units
Infants and very young children manipulate objects – pebbles, buttons, building blocks, or whatever they are given or find to play with. Frequently such play takes the form of assembling a collection in one place and then transferring it one by one to another place. These manipulations have been extensively observed and analyzed by Forman (1973; Forman, Kuschner & Dempsey, 1975).
Experientially – i.e. reconstructing the child’s experience not from an observer’s perspective but such as it might be from the child’s own point of view – there are obvious differences between a situation with one item and situations with two or three items. There is no problem about picking up one block; either hand can do it. When there are two, one hand may pick them up one after the other, but both hands are needed if the blocks are to be picked up simultaneously. If there are three, there is no way to pick them up simultaneously, but they can, of course, be picked up in succession. Although such considerations may seem trivial to an adult manipulator, they provide, in the case of the child, some important insights into what I call “protonumerical” processes and notions.
1. The simultaneous use of two hands in the displacement of two objects confers a very palpable difference to the visual and tactual experience of spatial configurations of one and two items rather than three or more.
2. The very fact that the same result of displacing two objects can be achieved by using one hand twice in temporal succession or by using both hands simultaneously, confers a very special status to the visual and tactual experience of two items. Moving both hands at the same time can be seen (whenever it is reflected on) as both a “single” and a “double” act, in that the motor component accentuates the singleness whereas its result accentuates the duality.
Though this experience may and does take place long before the infant has acquired any number words, let alone notions of numerosity, it is an experience that continually recurs during human life, simply because we have two hands and we sometimes use them separately and sometimes together. Hence there is in every (normal) child’s experience a host of situations from which to abstract the notion that configurations called “two” can be constructed or decomposed by taking “one” and then another “one”. As an empirical abstraction from sensorimotor experience, that notion constitutes solid protonumerical knowledge.
As the work of Steffe has shown, children learn the sequence of number-names and come to use it appropriately in counting sensory items quite some time before they acquire any awareness of the abstract units that constitute the components of numbers on the conceptual level (Steffe, Richards, & von Glasersfeld, 1979; Steffe & Thompson, 19 79). Thus kindergarten children, and as Gelman and Gallistel (1978) report, even three-year-olds, are able to coordinate the vocal production of the conventionally ordered string of number-words with the sequential tagging of perceptual items. Since this activity is generally fostered and rewarded by adults, who tend to take it as evidence of a far more advanced operating with numbers, children quickly become very good at this “apparent number skill” (Hatano, 1979). Among other things, they learn that this “counting” is considered the proper response to any question that contains the expression “How many?”, and that, in this context, success is greatly enhanced if they particularly stress or repeat the last number word of the string they are coordinating with the perceptual items. Although this has, as yet, nothing to do with a conception of number or numerosity,[13] it enhances the appearance of number skill which, in turn, assures reinforcement and, consequently, the proliferation of the “response”.
Once this verbal counting becomes something like a routine, it will interact, as Klahr and Wallace (1976) have pointed out, with the other activity that involves number-words: subitizing. This is quite inevitable in the case of those figural patterns that I have called iconic. These patterns – fingers, dominoes, playing cards – are configurations of countable perceptual items and the child therefore can, and at times will, count them. Whenever that happens the count will end with the very same number-word that has already been semantically associated as name with the figural pattern as a whole. That is to say, a dot pattern that has been called a “five” will yield “five” whenever the component dots are coordinated to the conventional string of number words. Such coincidences are unlikely to remain unnoticed. It will not take the child very long to discover that, while the connection between the word “five” and the numeral “5” cannot be confirmed by counting, the connection between the other (iconic) figural patterns and the names they have been given can be so confirmed. The discovery constitutes the first experiential root of the concept of numerosity or, indeed, cardinality (cf. Klahr & Wallace, 1976). The reason for this is that the coincidence of the number-word as terminal point of an iteractive procedure (i.e. the recitation and coordination of a fixed sequence of words) with the same number-word as result of a figural pattern perceived as a whole, provides an experiential foundation for the conception of number as a unit composed of units. The coordination of number-words to a succession of perceptual items requires that each item be conceived as a unit. No matter what sensory properties of the individual items are focused on, each item, in order to become the occasion for a vocal act in the recitation of number words, must be isolated and set apart from the rest of the experiential field, i.e., the item must be framed by the attentional pulses that constitute the unit structure. Similarly, however, the configuration of items, in order to be recognized as a whole, must also be framed by the attentional pulses that turn it, too, into a conceptual unit and, thus, it cannot but contain the others.
I emphasized that I am not suggesting that kindergarten children or first-graders are in any sense aware of the conceptual properties and relations involved in their construction of such units of units. But on the one hand their earliest protonumerical notions of single and dual motor acts were easily coordinated with figural patterns and with the number words “one” and “two” (and, by way of rhythmic repetitions of these acts, perhaps even with “three” and “four”); and on the other hand, children continue to subitize and to count as they grow older, and thus they continue to provide experiential situations from which, whenever they begin to reflect upon their own operating, they can reflectively abstract that crucial compositional aspect of the concept of number.
Experience of numerical relations
The second path towards the full conception of number is equally dependent on the phenomenon of subitizing but leads to a different yet no less “abstract” aspect. What I want to propose could be explicated with the help of any kind of perceptual items that happen to occur as the recursive element in configurations that are associated with the first few number words and are therefore likely candidates for subitizing. Because of their ubiquitous availability, I shall take the fingers of the hand; but what I say would apply equally to dot patterns or other configurations whose elements are always arranged and expanded according to simple composition rules (e.g. Brownell, 1928). When a child has to associate a certain finger pattern with the word “two” and another pattern with the word “four”, he or she can discover on the sensorimotor level (i.e. without any reference to numbers) that a “two” can be turned into a “four” by producing another “two”-configuration. Similar and even simpler will be the discovery that a “two” can be produced by joining a “one” to a “one” and so can a “three” if one starts with a “two”. For an adult, who cannot retrieve the procedures of his or her own infancy – simply because decades of experience have buried or obliterated them – it is practically impossible to see these combinations in a protonumerical, purely figural fashion; but there is every reason to believe that that is the only way a two or three-year-old sees them. In principle, the completion of a “three” configuration by joining a “one” to a “two” is no different from completing a face by drawing a mouth in a circle that already has a pair of eyes.
In other words, some relations analogous to those that characterize the conceptual system of whole numbers can be experientially acquired, without the concept of number, through the manipulation of perceptual patterns, their partition and composition. We have thus another instance of simple experiential situations that provide a basis for the future reflective abstraction of the second salient aspect of the constructs we call numbers: their interrelatedness in a homogeneous conceptual system.
It is this non-numerical, figural manipulation of perceptual items that Hatano has exploited in his system of early arithmetic instruction. He uses tiles and combines them to form linear configurations up to five. In his report (Hatano, 1979) he does not use the term “subitizing”, but it is clear that there is no counting; the configurations of two, three, four, and five are subitized by the children, and the transformations from one configuration to another are acquired perceptually and not numerically. Five was chosen as the initially most important upper limit, not because of the popularity of the abacus, but because it was found necessary.
“Without the intermediate unit of five, they (very young children) have considerable trouble trying to distinguish 6, 7, 8 and 9.
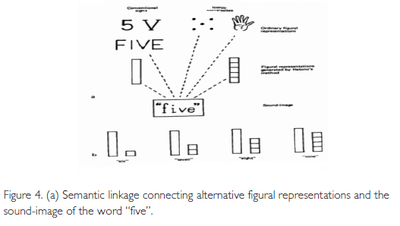
The use of five as an intermediate unit, adopting unsegmented tiles of five instead of continuous, connected or isolated tiles, makes it possible to represent these numbers as 5 + 1, 5 + 2, 5 + 3, (Fig. 4 b) respectively, and thus to grasp them almost intuitively, as different from others” (Hatano, 1979,p. 10; the reference to the Figure was changed to fit the numeration in this paper.)
In my terms , this means that first an alternative figural pattern is created and associated with the word “five” (see Figure 4 a); then the subsequent numbers 6, 7, 8, and 9 are presented as combinations of the “five”-pattern and the already familiar configurations called “one”, “two”, “three”, and “four”, respectively. This not only helps to differentiate the configurations which would be beyond the subitizing range if represented as configurations of single units, but it also makes the facts that a “six” is a “five” and a “one”, a “seven” is a “five” and a “two”, etc., perceptually accessible.[14] . I am deliberately using number words rather than numerals, to emphasize that I am referring to perceptual configurations (that happen to be associated with number words) and not to numerosities, let alone sets; and I am using the word “and” rather than the plus sign, to emphasize that I am referring to a figural joining and not to a numerical operation of addition.
(b) Easily recognizable configurations, whose figural representations can be associated with number words between “five” and “ten” (from Hatano, 1979).
In my view, the success of Hatano’s method is due above all to the fact that it supplies material that encourages the creation of stable, recursive, figural representations and sensorimotor activities such that they facilitate manipulation and composition and, beyond that, once the child comes to reflect upon them, they supply an optimal ground for the abstraction of numerical concepts and operations.
The process that Hatano engenders by the deliberate insertion of the intermediary unit “five” is analogous to the process Steffe has hypothesized on the basis of his observation of children who could reliably solve counting-on problems when the number to be counted-on was within the subitizing range (i.e. no larger than 5) but were invariably unable to solve those problems when the number was larger. Steffe explained this observation by the assumption that, as long as the child can produce for himself a figural, subitizable representation of the counting-on number, he can proceed to tick off the perceptual items contained in that representation as he continues the number word sequence from the given starting-point. In this way the child comes to an obligatory stop when he reaches the last item in the representation. When, on the other hand, the counting-on number is larger than 5, there is no ready figural representation for it and hence no way of ticking off and nothing to provide a stopping-point (Steffe, personal communication, 1978). Hatano’s method and Steffe’s observation of these counting-on episodes are examples that provide a perfect fit for the theoretical assumptions 1 have made.
There is one further point I want to stress. No matter how figural the deliberately encouraged activities may be, children are likely to persevere in the development of counting because, even if school makes no effort to foster it, everyday life and the social milieu will.[15] Hence children will count; that is to say, they will apply and coordinate the string of number words in an iterative fashion to the configurations they produce in perception or representation. In doing so, they create another occasion for the transition from the figural to the numerical, because through that activity the traditional order of the number-names can be seen figurally and numerically replicated in the ordered sequence of configurations: they get larger and more numerous as one goes on.[16] Thus also another abstract concept, namely ordinality, arises seemingly without break from a sensory-motor activity. What comes after “five” in the verbal sequence can be visually perceived as larger than “five” in the figural progression, and when the child then begins to count abstract units, the independently developed concepts of “after” and “larger” quite smoothly merge to form the abstract concept of the numerical “more”.
Summary and conclusion
This paper presents theoretical considerations concerning the roots of the conceptual development that contributes to the quantitative aspect of the constructs we call “number”. The effort is aimed at creating at least a preliminary structure of notions for the analysis of elementary processes that are in many ways taken for granted in investigations of early number skills and cognitive operations. The development of abstractions with which I am concerned is long and goes through many stages, but the focus of this paper is on the earliest beginnings, which may precede the counting and simple arithmetic tasks of first-graders by as much as four years; although these developments continue throughout childhood, their first inception is, I believe, characteristic for the entire itinerary which then, during the stage of formal operations, leads to truly mathematical thinking.
I argue that the adult conception of number is, indeed, a total abstraction consisting of elements that have been stripped of all sensorimotor properties (Piaget, 1970, p. 37; Piaget & Szeminska, 1967, p. 93); but I also agree with von Humboldt’s insight that we can “comprehend and hold” these abstractions only with the help of sensory material (cf. the motto of this chapter). Reflective abstraction is here taken literally: It lifts the construction pattern out of a sensorimotor configuration, leaving behind the actual sensory material – in other words, holding on to the connecting, relating, integrating operations, and disregarding the stuff that was connected by them.
The brief exposition of the conceptual model for the semantic link between single words and their meaning provides the basis for the discussion of subitizing as the perceptual recognition of certain recurrent configurations that are associated with number words. The fact that the same number words are elements of a conventional string that is acquired as a fixed sequence in auditory perception and vocal production, leads to peculiar coincidences in the experience of the child. Particular figural patterns that are already labeled with a number-name can be seen as collections of perceptual units that can be counted. Whenever that happens, the counting sequence ends with the number word that is already associated with the configuration as its object-name. In these cases the result of the child’s counting scheme turns out to be the same as the result of the naming scheme. While this is worked out in some detail for the visual perception of spatial configurations that are frequently referred to by names that are number-words, I suggest that temporal patterns, such as simple rhythms, are also involved in the process and that they constitute a further step towards the abstract conceptual structure of number as an iteration of attentional pulses.
Another aspect of the development is seen in the simple manipulations that infants perform with graspable objects. Here, too, we have situations where unitary configurations arise sometimes as a whole and at other times through the composition of parts.
The principle that instances of two or more schemes leading to one and the same result propel the child to a higher, more abstract level of operating is deeply embedded in Piaget’s theory of cognitive development (even if it is rarely made as explicit as its opposite, i.e., one scheme leading to two or more different results). That principle is crucial in the construction of “permanent” objects – where the spatial, temporal, and causal coordination of sensorimotor material culminates in the conception and representation of “existing” things, and it is crucial in the construction of invariants that are “conserved” – where sensorimotor experiences of “nothing added, nothing taken away”, instances of figural “using a bit of height to make more width”, and the scheme for “individual identity” are indispensable components of the abstract, operative conception of length, area, weight, etc.
I have tried to show that the same general principle of cognitive development applies to that part of the conception of “number” that constitutes it as a “unit of units”. From this perspective it is the unitary figural representation of a pattern, coinciding with the result of counting the elements of the pattern, that makes possible and leads to the conception of a number as consisting of countable components.
Thus, from the structural analysis of the concept of number in terms of attentional pulses (von Glasersfeld, 1981a), we have come a good deal further towards the full, mature construct that has numerosity. First, the infant’s manipulative actions with one hand or with both hands simultaneously, create an experiential difference between oneness and twoness. Second, the activity of subitizing constitutes oneness, twoness, up to fiveness as abstractions from figurally discriminable experiences that can also be “counted.” As Hatano’s practice suggests, the introduction of a subsidiary non-composite unit of “five” helps to extend the range of these figural patterns over the next few counting numbers and makes possible figural compositions and separations whose results are equivalent to addition and subtraction. But these first abstractions from figural patterns, and the equally figural acts of joining and separating, are not yet truly numerical operations. The numerical concepts proper, as I have argued earlier, are the result of abstraction from attentional patterns, not figural ones. Attentional patterns, however, do not normally occur in an experiential vacuum. Hence I contend that we first develop them on the basis of perceptions of figural patterns in space and time, their representations, and the abstraction of structural patterns from them. Only later, as a second step, do we abstract the attentional patterns whose unconscious “automatic” application to sensory material made the figurative compositions possible. Then and only then do we come to have “number” as an abstract unit of units that are themselves wholly abstracted from sensory-motor experience. We can then operate with the relations between these abstract entities and can represent them symbolically by means of numerals and letters. But whenever we want to comprehend them or visualize their specific numerosities, we switch back to the figural level and re-present to ourselves spatial configurations that we are able to see, or, alternatively, such temporal configurations as the nervous system can directly apprehend as rhythms or specific frequencies from which, finally, the iterative attentional patterns that constitute numerical concepts proper can be abstracted.
Acknowledgement
Although the basic theoretical principles applied in this paper are the result of some twenty years work in conceptual semantics and genetic epistemology, they could not have been applied in this way, nor could this paper have been written, were it not for the inspired micro-analyses of children’s behavior in counting and arithmetic that have been carried out by Les Steffe and his collaborators in educational research. I gratefully acknowledge his many helpful suggestions and the constructive criticism of a draft of the paper from him as well as from John Richards, Jack Lochhead, and Ricky Carter.
References
Bamberger, J. The development of musical intelligence: Children’s representation of simple rhythms (Artificial Intelligence Memo 342). Cambridge, MA: M.I.T. 1975.
Bamberger, J. Cognitive structuring in the apprehension and description of simple rhythms. Archives de Psychologie, 1980, 48, 171-197. (a)
Bamberger, J. Revisiting children’s drawings of simple rhythms: A function for reflection in-action. In S. Strauss (Ed ), U-Shaped behavior growth. New York: Academic Press, 1982.
Barrett, M.D. Lexical development and overextension in child language. Journal of Child Language, 1978, 5, 205-219.
Brownell, W. A. The development of children’s number ideas in the primary grades. Chicago: University of Chicago Press, 1928.
Czerny, P. & von Glasersfeld, E. A dynamic approach to the recognition of triangularity. Unpublished manuscript. University of Georgia, 1979.
Forman, G.E. The early growth of logic in children: Influences from the bilateral symmetry of human anatomy. Paper presented at the Biennial Meeting of SRCD, Philadelphia, 1973.
Forman, G.E., Kuschner, D.S., & Dempsey, J. Transformations in the manipulations performed with geometric objects: An early system of logic in young children. Final Report, Grant NE-G-00-3-0051, NIE, Washington, D.C., 1975.
Fuson, K.C. & Richards, J. Children’s construction of the counting numbers: From a spew to a bidirectional chain. Paper presented at AERA Meeting, Boston, 1980.
Gelman, R. & Gallistel, C.R. The child’s understanding of number. Cambridge, MA: Harvard University Press, 1978.
von Glasersfeld, E. Piaget and the radical constructivist epistemology. In C.D. Smock & E von Glasersfeld (Eds.), Epistemology and education. Athens, GA: Follow Through Publications, 1974.
von Glasersfeld, E. Radical constructivism and Piaget’s concept of knowledge(Presented at 5th Symposium of JPS, Philadelphia, 1975). In F.B. Murray (Ed.),
Impact of Piagetian theory. Baltimore: Univcrsity Park Press, 1979, pp. l09-122.(a)
von Glasersfeld, E. Cybernetics, experience, and the concept of self. In M.N. Ozer (Ed.), A cybernetic approach to the assessment of children: Toward a more humane use of human beings. Boulder, Colorado: Westview Press, 1979, pp. 67-113.(b)
von Glasersfeld, E. An attentional model for the conceptual construction of units and number. Journal for Research in Mathematics Education, 1981, 12, 83-94. (a)
von Glasersfeld, E. Sensory-motor sources of numerosity. Paper presented at 11th Symposium of the Jean Piaget Society, Philadelphia, May, 1981. (b)
von Glasersffld, E. The conception and perception of number. In S. Wagner & W.E. Geeslin (Eds.), Proceedings of the conference on mathematical and cognitive development. Columbus, Ohio: The Ohio State University, ERIC/SMEAC, 1981. (c)
von Glasersfeld, E. An interpretation of Piaget’s constructivism. Revue Internationale de Philosophie, 1982, 36 (4), 612-635.
Hatano, G. Learning to add and subtract: A Japanese perspective. Paper presented at the Wingspread Conference on Learning of Addition and Subtraction Skills, Racine, Wisconsin, Fall 1979.
Howell, H.B. A foundational study in the pedagogy of arithmetic. New York: Macmillan, 1914. von Humboldt, W. Prolegemena to philosophy of language (1796). Translation and commentary by N. Rotenstreich. Cultural Hermeneutics, 1974, 2, 211-227.
Husserl, E. Philosophie der Arithmetik (Original German text and revisions, 1887-1901). Den Haag: Nijhoff, 1970.
Katz, J.J., & Fodor, J.A. The structure of semantic theory. Language, 1963, 39, 1702l0.
Kaufman, E.L., Lord, M.W., Reese, T.W., & Volkmann, J. The discrimination of visual number. American Journal of Psychology, 1949, 62, 498-525.
Klahr, D., & Wallace, J.G. Cognitive development. Hillsdale, N.J.: Erlbaum, 1976.
Lemert, C.C. Language, structure, and measurement: Structuralist semiotics and sociology. American Journal of Sociology, 1979, 84, 929-957.
Mandler, G. & Shebo, B.J. Subitizing: An analysis of its component processes. Unpublished manuscript. University of California, San Diego, 1980.
Ogden, C.K., & Richards, I.A. The meaning of meaning. New York: Harcourt Brace, 8th edition, 1946, (Original edition, 1923)
Peirce, C.S. Collected papers of C.S. Peirce (Edited by C. Hartshorne & P. Weiss). Cambridge, MA: Harvard University Press, 1931 – 1935.
Piaget, J. La construction du réel chez l’enfant. Neuchâtel: Delachaux et Niestlé, 1937.
Piaget, J. Genetic epistemology. New York: Columbia U. Press, 1970.
Piaget, J. L’équilibration des structures cognitives. Paris: Presses Universitaires de France, 1975.
Piaget, J., & Szeminska, A. La genèse du nombre chez l’enfant. Neuchâtel: Delachaux et Niestlé, 4th edition, 1967. (Original edition, 1941)
Pollack, R.H., & Brenner, M.W. (Eds.) The experimental psychology of Alfred Binet. New York: Springer, 1969.
Pollio, H. R., & Whitacre, J .D. Some observations on the use of natural numbers by preschool children. Perceptual and Motor Skills, 1970, 30, 1967-1974.
Potter, M.C., & Levy, E.I. Spatial enumeration without counting. Child Development, 1968, 39, 265-272.
Richards, J., & von Glasersfeld, E. The control of perception and the construction of reality. Dialectica, 1979, 33, 37-58.
de Saussure, F. Course in general linguistics. New York: Philosophical Library, 1959. (Original edition, 1915)
Saxe, G.B. Childern’s counting: The early formation of numerical symbols. New Directions for Child Development, 1979, Nr.3, 73-84.
Schaeffer, F., Eggleston, V.H., & Scott, J.L. Number development in young children. Cognitive Psychology, 1974, 6, 357-379.
Starkey, P., & Cooper, R.J. Perception of numbers by human infants. Science, 1980, 210, 1033-1035.
Steffe, L.P., von Glasersfeld, E., Richards, J., & Cobb, P. Children’s counting types: Philosophy, theory, and application. New York: Praeger, 1983.
Steffe, L.P., Richards, J., & von Glasersfeld, E. Experimental models for the child’s acquisition of counting and of addition and subtraction. In K.C. Fuson & W.E.
Geeslin (Eds.), Explorations in the modeling of the learning of mathematics. Columbus, Ohio: The Ohio State University, ERIC/SMEAC, 1979, pp. 27-44.
Steffe, L.P. & Thompson, P. Children’s counting in arithmetical problem solving. Paper presented at the Wingspread Conference on Learning of Addition and Subtraction Skills, Racine, Wisconsin, Fall 1979.
Stern, C. Children discover arithmetic. New York: Harper & Row, 1971.
Wirtz, R. New beginnings. Monterey, CA: Curriculum Development Associates, 1980.
No thinking, not even the Purest, can take place but with the aid of the universal forms of our sensua1ity; only in them can we comprehend it and, as it were, hold fast. – Wilhelm von Humboldt, 1796.[2]
It is this non-numerical, figural manipulation of perceptual items that Hatano has exploited in his system of early arithmetic instruction. He uses tiles and combines them to form linear configurations up to five. In his report (Hatano, 1979) he does not use the term “subitizing”, but it is clear that there is no counting; the configurations of two, three, four, and five are subitized by the children, and the transformations from one configuration to another are acquired perceptually and not numerically. Five was chosen as the initially most important upper limit, not because of the popularity of the abacus, but because it was found necessary.
“The essence of thinking consists in reflecting, i.e., in distinguishing the thinking from that which is thought about” (von Humboldt, translation by Rotenstreich, 1974, p. 211).
Once semantic connections are beginning to be formed, any recurrent figural pattern can be semantically associated with a number word. That children actually do this, has been observed quite frequently (e.g. Wirtz,1980,p.2).
Number words are words and, as happens with other words, children can learn to say them long before they have formed perceptual representations, let alone abstract concepts to associate with them (in Fig. 2, this corresponds to establishing the straight connections B and G prior to the connections D and E). The learning of empty, as yet meaningless words is easier and more likely when the words have a fixed order in which they frequently occur. That is, of course, the case with number words as well as with the rhymes and prayers which children can learn without the least understanding. Piaget remarked long ago that the reciting of the initial string of number words is usually imposed on children at a very early stage (i.e. before they are four years old) but is then “entirely verbal and without operational significance” (Piaget & Szeminska, 1967, p. 48; cf. also Pollio &: Whitacre, 1970 Potter & Levy, 1968; Saxe, 1979).
At an even earlier age, however, children may learn a few isolated number words in the same way in which they learn object-words. It usually happens with the first number words of the conventional sequence, at least from “one” through “five”; and since those are the very ones that are then used in subitizing, we have to ask how words of any kind are initially acquired. A twelve-month-old may come to associate the auditory experience of the word “spoon” (recurrently uttered by mother) with the global sensorimotor experience of being spoon-fed or trying to feed himself. He may then attempt to reproduce the auditory experience through vocal act of his own. By the age of 24 months, at any rate, the child will have segmented and organized his or her sensorimotor experience quite sufficiently to recognize the spoon in the visual field alone (without tactual or motor complements) and from any angle. Indeed, the spoon will have become a “permanent object” (Piaget, 1937) with characteristic visual pattern and other sensorimotor aspects that can be called up as a representation when the object is not in sight, and that representation will have a firm semantic connection with the sounde-image of the word “spoon” (connection D in Fig. 2).
Once semantic connections are beginning to be formed, any recurrent figural pattern can be semantically associated with a number word. That children actually do this, has been observed quite frequently (e.g. Wirtz,1980,p.2).Once this verbal counting becomes something like a routine, it will interact, as Klahr and Wallace (1976) have pointed out, with the other activity that involves number-words: subitizing. This is quite inevitable in the case of those figural patterns that I have called iconic.
In their classic work The Meaning of Meaning, Ogden and Richards (1946) drastically simplified that arrangement by compounding (and thus confounding) “concept” and “sound-image “at the apex of a triangle whose lower corners pointed at “referent” (object) and “symbol” (word) respectively.
“It [language] is a system of signs in which the only essential thing is the union of meanings and sound-images, and in which both parts of the sign are psychological” (de Saussure, 1959, p. 15). “The linguistic sign unites, not a thing and a name, but a concept and a soundimage” (ibid., p. 66).
As the work of Steffe has shown, children learn the sequence of number-names and come to use it appropriately in counting sensory items quite some time before they acquire any awareness of the abstract units that constitute the components of numbers on the conceptual level (Steffe, Richards, & von Glasersfeld, 1979; Steffe & Thompson, 19 79).
Infants and very young children manipulate objects – pebbles, buttons, building blocks, or whatever they are given or find to play with. Frequently such play takes the form of assembling a collection in one place and then transferring it one by one to another place. These manipulations have been extensively observed and analyzed by Forman (1973; Forman, Kuschner & Dempsey, 1975).
The use of five as an intermediate unit, adopting unsegmented tiles of five instead of continuous, connected or isolated tiles, makes it possible to represent these numbers as 5 + 1, 5 + 2, 5 + 3, (Fig. 4 b) respectively, and thus to grasp them almost intuitively, as different from others” (Hatano, 1979,p. 10; the reference to the Figure was changed to fit the numeration in this paper.)
The second path towards the full conception of number is equally dependent on the phenomenon of subitizing but leads to a different yet no less “abstract” aspect. What I want to propose could be explicated with the help of any kind of perceptual items that happen to occur as the recursive element in configurations that are associated with the first few number words and are therefore likely candidates for subitizing. Because of their ubiquitous availability, I shall take the fingers of the hand; but what I say would apply equally to dot patterns or other configurations whose elements are always arranged and expanded according to simple composition rules (e.g. Brownell, 1928). When a child has to associate a certain finger pattern with the word “two” and another pattern with the word “four”, he or she can discover on the sensorimotor level (i.e. without any reference to numbers) that a “two” can be turned into a “four” by producing another “two”-configuration. Similar and even simpler will be the discovery that a “two” can be produced by joining a “one” to a “one” and so can a “three” if one starts with a “two”. For an adult, who cannot retrieve the procedures of his or her own infancy – simply because decades of experience have buried or obliterated them – it is practically impossible to see these combinations in a protonumerical, purely figural fashion; but there is every reason to believe that that is the only way a two or three-year-old sees them. In principle, the completion of a “three” configuration by joining a “one” to a “two” is no different from completing a face by drawing a mouth in a circle that already has a pair of eyes. In other words, some relations analogous to those that characterize the conceptual system of whole numbers can be experientially acquired, without the concept of number, through the manipulation of perceptual patterns, their partition and composition. We have thus another instance of simple experiential situations that provide a basis for the future reflective abstraction of the second salient aspect of the constructs we call numbers: their interrelatedness in a homogeneous conceptual system.
The same process has been described and analyzed by Husserl in 1890[7] and Piaget has used the term “reflective abstraction” all along, distinguishing it from “empirical abstraction”. Recently (Piaget, 1975, p. 63) he has come to the conclusion that the two types of abstraction take place in constant interaction. For the purpose of explication, however, it is helpful to present the two levels of abstraction sequentially, even if in the child’s actual development there is, as Piaget now says, frequent reciprocal interaction between them.
In short, then, I am suggesting that the infants’ ability to distinguish between linear displays of one, two, and three dots (Starkey & Cooper, 1980), young children ‘s facility for depicting auditory patterns graphically (Bamberger, 1975), the telegraphist’s skill of translating visual into motor sequences, and, finally, the general ability to subitize linear arrangements of perceptual items, can all be reduced to an underlying capacity to distinguish, recognize, and represent simple temporal configurations that have a characteristic iterative structure.
Number and numerosity, thus, do have a root in the processing of percepts and hence there arises the question of how that involvement comes about. I am proposing the thesis that there are several experientially independent paths that contribute to the generation of the complex conceptual structure that we, as adults, ordinarily call number. All three paths contribute to the adult concept, but none of them entails the pursuit of the others.
Before attempting to delineate these paths, let me justify the emphasis on the complexity of the number concept. In an earlier paper (1981a) I presented an attentional model for the structure of number concepts and concentrated on the material out of which such concepts may be formed, namely attentional pulses. I explicitly stated that although the products of the attentional construction have numerosity, their structure must not be confused with the concept of numerosity. That distinction is particularly important because, ordinarily, when we use the word “number” we do not specify whether we are speaking of a numerical structure or of its numerosity. The difference may become more palpable if we compare it to a logically analogous difference in another area. The colors we perceive can be correlated to the frequency of waves which we postulate as the structure of light. If we then say yellow lies between such and such frequencies, we are talking about the structure of yellow, not about the characteristic quality of yellowness that we distinguish from orange and green. Although we can correlate wave lengths and frequencies with our experience of color, they tell us nothing about that experience, nor why it should change as we move along the frequency scale, why we see blue as we move up from green, and red as we move down from orange. Similarly, the attentional model provides a way of thinking about the structure of number concepts but, by itself, it tells us nothing about what we call “quantity” or “numerosity”.
Unlike the color analogy, where there is, at present, no way at all of relating the qualitative experience to any structural model, I shall suggest in what follows how the conception of numerosity can be related to the attentional model of number. I have stressed the complexity of number concepts because, in the view presented here, they comprise, on the one hand, an attentional structure that characterizes all of them – analogous to the wave notion that characterizes the structure of all colors – and, on the other hand, a conception of numerosity that is itself a composite of the products of several relatively independent conceptual developments.What de Saussure said can be complemented by a simple diagram that shows that the “semantic connection” is always on the experiencer’s side of the experiential interface and not in what is often called the “objective environment” (see Fig. 1). De Saussure’s term “sound-image” refers to conceptual representations abstracted from the experience of spoken words and is, thus, analogous to “concept” which refers to conceptual representations of non-verbal experiences. Reality and the items considered part of it, are put between quotation marks because, from the constructivist perspective, they are an observer’s externalized percepts rather than “real” things or events in an observer-independent ontological world (cf. von Glasersfeld, 1974; Richards & von Glasersfeld, 1979).
Experientially – i.e. reconstructing the child’s experience not from an observer’s perspective but such as it might be from the child’s own point of view – there are obvious differences between a situation with one item and situations with two or three items. There is no problem about picking up one block; either hand can do it. When there are two, one hand may pick them up one after the other, but both hands are needed if the blocks are to be picked up simultaneously. If there are three, there is no way to pick them up simultaneously, but they can, of course, be picked up in succession. Although such considerations may seem trivial to an adult manipulator, they provide, in the case of the child, some important insights into what I call “protonumerical” processes and notions.
1. The simultaneous use of two hands in the displacement of two objects confers a very palpable difference to the visual and tactual experience of spatial configurations of one and two items rather than three or more. 2. The very fact that the same result of displacing two objects can be achieved by using one hand twice in temporal succession or by using both hands simultaneously, confers a very special status to the visual and tactual experience of two items. Moving both hands at the same time can be seen (whenever it is reflected on) as both a “single” and a “double” act, in that the motor component accentuates the singleness whereas its result accentuates the duality.
Though this experience may and does take place long before the infant has acquired any number words, let alone notions of numerosity, it is an experience that continually recurs during human life, simply because we have two hands and we sometimes use them separately and sometimes together. Hence there is in every (normal) child’s experience a host of situations from which to abstract the notion that configurations called “two” can be constructed or decomposed by taking “one” and then another “one”. As an empirical abstraction from sensorimotor experience, that notion constitutes solid protonumerical knowledge.There are dot patterns and other spatial configurations that are obviously not distinguishable on the basis of qualitative motor characteristics of scan-paths. If two dots are recognized as a characteristic configuration by the sole fact that they are connected by a straight scan-path, then three, four, or more dots in linear arrangement would be considered the same. Yet this is not the case. Starkey and Cooper (1980) have elegantly shown that even infants of less than six months discriminate quite reliably three dots in a line from two, whereas they do not seem to discriminate between four and six. We may safely assume that infants of that age cannot count. On the other hand, the experiment made clear that the discrimination does not depend on the distance between the dots or on the over-all extension of the display. Hence there must be some inherent difference in the process of perceiving two as opposed to three dots.[11] That difference, I suggest, arises from the capability of the nervous system to differentiate between the temporal patterns constituted by a succession of two perceptual acts as opposed to one or three. “Perceptual act” in this context means no less and no more than the isolation of any item whatever from the rest of the experiential field which, in the case at hand, can be reduced to the visual field. In other words, I am positing a neural mechanism that distinguishes a dual incidence of a given event from a single or a treble incidence (von Glasersfeld, 1981b). What will be considered a dual event, rather than two single ones in succession, depends of course on temporal parameters which we must assume to be inherent in the system – an assumption that can not be invalidated by the observation that these temporal parameters can, under certain circumstances, be modified by experience, practice, or training.
The best-known instances of non-numerical discrimination and recognition of single, dual, treble, etc., events are probably those that occur when we listen to music, where they form the experiential material that goes by the name of “rhythm”. Recent work with children leaves no doubt that the ability to remember, recognize, and replicate simple rhythms (by clapping or tapping) is manifested prior to any abstract or notational representations of such rhythms (Bamberger, 1975, 1980, 1982). That is to say, a sequence of beats which an adult might capture in a conventional notation, is recognized by the child as a figural pattern in a way analogous to that in which visual shapes are first recognized, but with the difference that the rhythm is a configuration in time, whereas the shapes appear as configurations in space (von Glasersfeld, 1979b). From my point of view, it is particularly interesting that the children in that study had little or no difficulty in “drawing” the rhythms by inventing their own visual representations. This readiness to translate a temporal pattern into a linear spatial one strongly supports my assumption that the visual perception of a linear arrangement of items can, indeed, be characterized (and distinguished from other visual experiences of the kind) by its rhythmic properties. In both vision and audition the temporal pattern is constituted by a sequence of perceptual acts which are given their structure by a succession of attentional pulses. This is rather obvious in auditory experience, which is necessarily perceived as an ordered sequence of events in time. In visual experience the sequentially is obscured because, under most circumstances, the individual perceptual acts that constitute a spatial configuration are not subject to an obligatory order.[12] That is why linear arrangements are something of a special case: There, a definite order is at least strongly suggested by the ease and economy of the linear scan-path. A striking example of the ability to transpose spatial into temporal patterns is the telegraphist’s translation of written Morse code into a sequence of motor acts that make and break an electric contact. Here the conventional order of the left to-right line is turned into a temporal order. The groups of dots and dashes on the source tape are neither counted nor perceived as numerical structures – they are taken as patterns of perceptual acts that can be immediately realized in terms of motor acts because the rhythmic configuration remains experientially the same in both modes. In short, then, I am suggesting that the infants’ ability to distinguish between linear displays of one, two, and three dots (Starkey & Cooper, 1980), young children ‘s facility for depicting auditory patterns graphically (Bamberger, 1975), the telegraphist’s skill of translating visual into motor sequences, and, finally, the general ability to subitize linear arrangements of perceptual items, can all be reduced to an underlying capacity to distinguish, recognize, and represent simple temporal configurations that have a characteristic iterative structure. Such iterative structures have rhythmic patterns that can be empirically abstracted as figural patterns from sensory events, not only in the auditory mode, but also in the kinesthetic, tactual, and visual modes, because, in all these modes of experience, structure is constituted by a patterned succession of attentional moments that was experientially determined by the sequence of sensory signals. Once abstracted, these rhythmic patterns may be semantically associated with number-words. The link to a number word, however, does not turn them into numerical concepts. Conceptually they are still figural patterns. Only “reflective” abstraction – the focusing of attention on their iterative structure rather than on the actual or representational sensory material with which that structure happens to have been implemented – can raise them to the level of “pure” abstraction that is characteristic of the conception of numbers (von Glasersfeld, 1981a).
On the other hand, already as figural patterns consisting of sequences of perceptual items, representations of such rhythmic structures make possible the recognition of specific sequential configurations of dots, checkers, fingers, etc., as instances of patterns that are associated with one of the number-words between one and five. Thus, analogous to the way in which a characteristic scan-path serves as the criterial recognition feature for specific classes of spatial patterns (e.g. triangles), a characteristic rhythmic structure serves as the criterial recognition feature for large classes of sensory events which, experientially, can be reduced to temporal patterns. Since these classes comprise not only auditory and motor events (whose nature is sequential in any case), but also visual and tactual events whose sequentiality is created by a relatively fixed linear order of the perceptual process, the recognition of rhythmic structures plays an important role in the phenomenon of subitizing and as a necessary precondition to the reflective abstraction of numerical concepts from linear configurations of items such as dots and tiles, and from Finger patterns.(b) Easily recognizable configurations, whose figural representations can be associated with number words between “five” and “ten” (from Hatano, 1979).
In my view, the success of Hatano’s method is due above all to the fact that it supplies material that encourages the creation of stable, recursive, figural representations and sensorimotor activities such that they facilitate manipulation and composition and, beyond that, once the child comes to reflect upon them, they supply an optimal ground for the abstraction of numerical concepts and operations.
The process that Hatano engenders by the deliberate insertion of the intermediary unit “five” is analogous to the process Steffe has hypothesized on the basis of his observation of children who could reliably solve counting-on problems when the number to be counted-on was within the subitizing range (i.e. no larger than 5) but were invariably unable to solve those problems when the number was larger. Steffe explained this observation by the assumption that, as long as the child can produce for himself a figural, subitizable representation of the counting-on number, he can proceed to tick off the perceptual items contained in that representation as he continues the number word sequence from the given starting-point. In this way the child comes to an obligatory stop when he reaches the last item in the representation. When, on the other hand, the counting-on number is larger than 5, there is no ready figural representation for it and hence no way of ticking off and nothing to provide a stopping-point (Steffe, personal communication, 1978). Hatano’s method and Steffe’s observation of these counting-on episodes are examples that provide a perfect fit for the theoretical assumptions 1 have made.There is one further point I want to stress. No matter how figural the deliberately encouraged activities may be, children are likely to persevere in the development of counting because, even if school makes no effort to foster it, everyday life and the social milieu will.[15] Hence children will count; that is to say, they will apply and coordinate the string of number words in an iterative fashion to the configurations they produce in perception or representation. In doing so, they create another occasion for the transition from the figural to the numerical, because through that activity the traditional order of the number-names can be seen figurally and numerically replicated in the ordered sequence of configurations: they get larger and more numerous as one goes on.[16] Thus also another abstract concept, namely ordinality, arises seemingly without break from a sensory-motor activity. What comes after “five” in the verbal sequence can be visually perceived as larger than “five” in the figural progression, and when the child then begins to count abstract units, the independently developed concepts of “after” and “larger” quite smoothly merge to form the abstract concept of the numerical “more”.
In their classic work The Meaning of Meaning, Ogden and Richards (1946) drastically simplified that arrangement by compounding (and thus confounding) “concept” and “sound-image “at the apex of a triangle whose lower corners pointed at “referent” (object) and “symbol” (word) respectively. Strongly influenced by the rise of behaviorism they apparently were uneasy about “mental” constructs such as concepts and sound-images but they still felt the need to put the word “thought” at the apex of their triangle and it is certainly to their credit that they emphasized the fact that the direct connection between symbol and objective referent is an imagined or “purported” one. However, their simplification was an unfortunate step in the direction of radical Behaviorism, the school that later flourished and tried to eliminate thought altogether and to substitute a directly connected “stimulus” and “response” for symbols and referents. It has taken a long time to overcome this categorical elimination of mental operations and meaning, both in linguistics and in psychology. But now the general attitude has changed and we may once more adopt the view held at the beginning of the century when not only de Saussure but also Charles Peirce had realized that symbols and their referents could have no connection other than that formed in the minds of symbol users. Rather than simplify the schematic arrangement of de Saussure’s “psychological” connection between words and things we must amplify it considerably before we can adopt it as plausible model of the human word processor. For the present purpose it will suffice to say that such a model must include the step from percepts to representations and the step from representations to motor programs for the production of utterances (see Fig. 2)
As the work of Steffe has shown, children learn the sequence of number-names and come to use it appropriately in counting sensory items quite some time before they acquire any awareness of the abstract units that constitute the components of numbers on the conceptual level (Steffe, Richards, & von Glasersfeld, 1979; Steffe & Thompson, 19 79). Thus kindergarten children, and as Gelman and Gallistel (1978) report, even three-year-olds, are able to coordinate the vocal production of the conventionally ordered string of number-words with the sequential tagging of perceptual items. Since this activity is generally fostered and rewarded by adults, who tend to take it as evidence of a far more advanced operating with numbers, children quickly become very good at this “apparent number skill” (Hatano, 1979). Among other things, they learn that this “counting” is considered the proper response to any question that contains the expression “How many?”, and that, in this context, success is greatly enhanced if they particularly stress or repeat the last number word of the string they are coordinating with the perceptual items. Although this has, as yet, nothing to do with a conception of number or numerosity,[13] it enhances the appearance of number skill which, in turn, assures reinforcement and, consequently, the proliferation of the “response”. Once this verbal counting becomes something like a routine, it will interact, as Klahr and Wallace (1976) have pointed out, with the other activity that involves number-words: subitizing. This is quite inevitable in the case of those figural patterns that I have called iconic. These patterns – fingers, dominoes, playing cards – are configurations of countable perceptual items and the child therefore can, and at times will, count them. Whenever that happens the count will end with the very same number-word that has already been semantically associated as name with the figural pattern as a whole. That is to say, a dot pattern that has been called a “five” will yield “five” whenever the component dots are coordinated to the conventional string of number words. Such coincidences are unlikely to remain unnoticed. It will not take the child very long to discover that, while the connection between the word “five” and the numeral “5” cannot be confirmed by counting, the connection between the other (iconic) figural patterns and the names they have been given can be so confirmed. The discovery constitutes the first experiential root of the concept of numerosity or, indeed, cardinality (cf. Klahr & Wallace, 1976). The reason for this is that the coincidence of the number-word as terminal point of an iteractive procedure (i.e. the recitation and coordination of a fixed sequence of words) with the same number-word as result of a figural pattern perceived as a whole, provides an experiential foundation for the conception of number as a unit composed of units. The coordination of number-words to a succession of perceptual items requires that each item be conceived as a unit. No matter what sensory properties of the individual items are focused on, each item, in order to become the occasion for a vocal act in the recitation of number words, must be isolated and set apart from the rest of the experiential field, i.e., the item must be framed by the attentional pulses that constitute the unit structure. Similarly, however, the configuration of items, in order to be recognized as a whole, must also be framed by the attentional pulses that turn it, too, into a conceptual unit and, thus, it cannot but contain the others.
The hypothesis of alternative figural representations that are “equivalent” in that they are all semantically connected to one word, has the virtue that it at once fits how children come to recognize a considerable variety of figural patterns as legitimate referents of a number word long before they have any conception of number or numerosity. The sound image of “three” is easily associated with whatever perceptual configurations are explicitly called “three” by the adults in whose company the child grows up. There will be finger patterns, patterns of dots and lines, arrangements of particular design elements (hearts, diamonds, etc.), and of course the variations of the numeral 3. Some of these figural patterns area “iconic” in that they are composites of perceptual units which, if considered quantitatively (by a counter who already has numerical concepts) represent the numerosity designated by the number word with which they are associated. Others, like the Arabic numerals (and the Roman numerals above III) are not iconic, because they are not constituted by a collection of items that has the indicated numerosity. Thus I am suggesting that, in subitizing, the child associates figural patterns with number words by a semantic connection and not because of the number of perceptual units of which they are composed. In acts of subitizing, the figural patterns that give rise to it are taken as figural wholes and not as composites of units. In fact, they are recognized as a global configuration, not as a collection of countable items.
Piaget and Szeminska characterized it well when they said that, for instance, the corner points of a triangle correspond to the corner points of other triangles, irrespective of the knowledge that their number is the same – just as the parts of one human face correspond to those another (1967, p. 93).
Thus kindergarten children, and as Gelman and Gallistel (1978) report, even three-year-olds, are able to coordinate the vocal production of the conventionally ordered string of number-words with the sequential tagging of perceptual items. Since this activity is generally fostered and rewarded by adults, who tend to take it as evidence of a far more advanced operating with numbers, children quickly become very good at this “apparent number skill” (Hatano, 1979).
Starkey and Cooper (1980) have elegantly shown that even infants of less than six months discriminate quite reliably three dots in a line from two, whereas they do not seem to discriminate between four and six.
The work of Brownell, who undertook a monumental study of the “apprehension of visual concrete number” (1928), contains many observations that indicate children’s preferential association of specific configurations with certain numbers and that the fact that figural regularities facilitate the “apprehension” of the correct numerosity. Unfortunately Brownell started from the realist assumption that numbers are “concrete” and can therefore be perceptually “apprehended”. Hence he assumed that, no matter how, say, four elements were arranged in space, the perception of their number would always be the same task, and he took great care to average the measurements obtained with different “sensory material”. Indeed, he criticized the earlier study by Howell (1914) because it used only one type of “number pictures”, namely the quadratic type, which represents numbers by placing dots in the corners of imaginary squares.
“permanent object” (Piaget, 1937)
Piaget remarked long ago that the reciting of the initial string of number words is usually imposed on children at a very early stage (i.e. before they are four years old) but is then “entirely verbal and without operational significance” (Piaget & Szeminska, 1967, p. 48; cf. also Pollio &: Whitacre, 1970 Potter & Levy, 1968; Saxe, 1979).
Though there have been theories that suggested it (e.g. Katz & Foder, 1963), it is utterly inconceivable that a child actually forms a universal representation of dog percepts when he or she discovers that adults use the word “dog” to refer, not only to his poodle, but also to a Dachshund, a Great Dane, a St. Bernard, and a bulldog. No common figural representation could cover that variety of canines without erroneously including members of other species as well (cf. Barrett, 1978).
The discovery constitutes the first experiential root of the concept of numerosity or, indeed, cardinality (cf. Klahr & Wallace, 1976).
Even if that expectation is fulfilled by many children, the fact that some fulfill it slowly and others not at all, raises the question of how one could specify more precisely what it is that has to be done.
Two earlier papers from our research group dealt with some aspects of that question. The first presented an analysis of counting types that explicated the development of the ability to count abstract unit items that may have been derived from, but are no longer dependent on, sensorimotor material (Steffe, Richards, & von Glasersfeld, 1979), the second a theoretical model for the abstract conceptual structures called “unit” and “number” (von Glasersfeld, 1981 a).
In the pages that follow I shall focus on the phenomenon of “subitizing” which has been known a long time but was usually treated as an oddity that is at best marginal in the acquisition of numerical skills.[3] Steffe’s large-scale investigations of children’s progress towards arithmetic competence, however, strongly suggest that perceptual recognition and subsequent representation of small lots up to four or five elements play an indispensable role in the development of arithmetic operations (Steffe, von Glasersfeld, Richards & Cobb, in prep.).[4]Only “reflective” abstraction – the focusing of attention on their iterative structure rather than on the actual or representational sensory material with which that structure happens to have been implemented – can raise them to the level of “pure” abstraction that is characteristic of the conception of numbers (von Glasersfeld, 1981a).
Since such characteristic paths can be abstracted as figural representations of “twos”, triangular “threes”, quadrilateral “fours”, and certain “fives”, they reduce the number of individual figural representations that have to be remembered in the case of spatial patterns consisting of up to five perceptual units. And this economy is achieved without any reference to number, nor is the concept of numerosity involved in the procedure (cf. Mandler & Shebo, 1980).
Numerical concepts, as Piaget and Szeminska (1967; Piaget, 1970) and many others have pointed out, are stripped of all sensorimotor properties and, therefore, necessarily involve reflective abstraction. A way to obtain wholly abstract numerical concepts that are independent not only of sensorimotor material but also of figural patterns, was proposed in an earlier paper (von Glasersfeld, 1981a).
Recent work with children leaves no doubt that the ability to remember, recognize, and replicate simple rhythms (by clapping or tapping) is manifested prior to any abstract or notational representations of such rhythms (Bamberger, 1975, 1980, 1982).
- ↑ The research summarized in this paper was supported by NSF Grant SED80-16562 and by the Department of Psychology of the University of Georgia.
- ↑ The motto is taken from Nathan Rotenstreich’s (1974) translation.
- ↑ The term “subitizing” was introduced by Kaufman, Lord, Reese and Volkmann (1949), who reviewed early literature on the perceptual recognition of “number” in visual arrays composed of a plurality of similar items. A more recent survey of literature and experimental demonstration of the phenomenon is provided by Mandler and Shebo (1980).
- ↑ That five constituted the upper limit for a four-year-old’s ability to apply number-names to configurations of objects was noticed already by Binet in his interesting studies on the “perception of number” (Pollack & Brenner, 1969, p.89).
- ↑ De Saussure has been rediscovered and partially exploited several times since then. Most recently some of his basic ideas have been adopted by sociologists (cf. Lemert, 1979).
- ↑ I want to emphasize that “representation” in the constructivist view never refers to a picture of an experiencer-independent “outside” world; instead it is intended literally to indicate a reconstruction of something that has been constructed at some prior experiential situation. Also the word “concept” must not be understood in the way in which it has frequently been used by learning psychologists, i.e. as referring simply to a perceptual dimension such as color, shape, size, etc.; instead, “concept” refers to any structure that has been abstracted from the process of experiential construction as recurrently usable, for instance, for the purpose or relating of classifying experiential situations. To be called “concept” these constructs must be stable enough to be re-presented in the absence of perceptual “input”.
- ↑ Husserl provided the following definition:” . . . we are dealing with mental acts of higher order, i.e., mental acts directed towards mental acts and only through their medium towards primary (perceptual) contents” (1970, p. 92; my translation).
- ↑ Note that this is seen from the perspective of a child growing into a linguistic community, i.e. a community in which a great many associations between experiential items and specific sound-images must be acquired by any prospective member. Such a community can and does, of course, establish new “arbitrary” semantic connections by some form of agreement (cf. do Saussure, 1959, pp. 67ff), but a child, or any single member of the community, cannot do that on his or her own.
- ↑ This was recently demonstrated by writing a very simple program for a minicomputer that faultlessly “recognized” triangles, without the use of any geometric criteria, exclusively on the bases of the movements carried out in scanning (Czerny & von Glasersfeld, 1979).
- ↑ Observations made by Schaeffer, Egglestone, and Scott ( 1974, p. 371 ) confirm that certain configurations are most easily associated with number words and, as it happens, these configurations are those that one would expect on the basis of the scan-path explanation given above.
- ↑ I stress the process of perceiving because, as I have shown elsewhere (von Glasersfeld, 1974, 1979a, 1979b, and 1981c), even from the perspective of a realist epistemology that assumes that “twoness”, “threeness”, etc., exist in an experiencer-independent world, any perceiving organism must still construct the patterns and concepts in terms of which it perceives that world. There is no conceivable path that could bring patterns or, indeed, any structured “information” into a cognizing system in one piece.
- ↑ This elementary contrast between the inevitable sequentiality of auditory experience and the arbitrary sequencing in visual experience is closely connected with the distinction Bamberger (1982) has made between “reflection of action” and “reflection on action”, a distinction that will undoubtedly be useful in the dark area of Piaget’s prise the conscience.
- ↑ Gelman and Gallistel (1978) call this apparent number skill “cardinal principle” (p. 79ff) and this somewhat inflated interpretation consequently leads them to the conclusion that “for the child as young as 2 1/2 years, enumeration already involves the realization that the last numberlog in a set – at least in a small set – represents the cardinal number of the set” (p. 98). Similarly Schaeffer et all (1974, p. 360) write: “Evidence that he, the child, knew that the last number he names during counting denoted the number of chips in the line (the cardinality rule) was that he could respond by naming the last number he had just counted”. The behaviors specified as criteria in these two “operational definitions of cardinality” are, from my point of view, not sufficient to infer any knowledge of “maniness” or numerosity The same disbelief is expressed by Fuson and Richards (1980).
- ↑ The creation of the alternative figured pattern for “five”, which serves as a means to extend the range of subitizable collections, sets Hatano’s method apart from that of Wirtz (1980} and a similar earlier system developed by Catherine Stern in the 1930s (Stern, 1971).
- ↑ Hatano (1979) reports that “parents want their children to acquire some number skills before grade 1” and that a large percentage of mothers “were teaching number skills whenever they found appropriate opportunities” (p.2). Western mothers may do less in that respect, but the social environment of a consumer society and the games children play in the West will make up for it.
- ↑ This, I believe, is what Fuson and Richards (1980, p.22) have in mind when they say that experiences of counting words isolated from the counting sequence are ““ot lost on the child and are incorporated into the sequence.”