Text:Radical Constructivism and Teaching
Published in French in Perspectives 31 (2): 191–204, 2001. This paper was downloaded from the Ernst von Glasersfeld Homepage, maintained by Alexander Riegler. It is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/2.0/ or send a letter to Creative Commons, 559 Nathan Abbott Way, Stanford, CA 94305, USA. Preprint version of 13 Feb 2006
Abstract
Learning will be defined as a conceptual activity and teaching distinguished from training. The role of language in these processes will be examined. The author maintains that there can be no understanding without reflection. Reflection is induced by verbalization and can therefore be encouraged by fostering conversation. Ceccato’s notion of ‘operational awareness’ will be shown to be relevant to teaching and compatible with Piaget’s theoretical model.
Radical Constructivism and Teaching
Introduction
I want to stake out my topic a little wider than is usual in papers on education. Inevitably, teachers are day in, day out concerned with the practical problems raised by the fact that the students’ learning is so often far below their expectations. They have little time to ponder some of the fundamental problems of their calling. And there is today no shortage of fundamental problems. Indeed there are more than could be dealt with in one presentation.
I shall restrict myself to two which I consider the most pressing. The first is the question of what we consider to be the purpose of education; the second is the more fundamental query of what ‘knowledge’ means from the constructivist perspective, and how this school of thought views the possibilities of its acquisition.
What is the Purpose of Education?
Education is a wide-ranging concept that may comprise training and formation, coaching in specialized competencies, fostering the ability to think, promoting manners, culture, taste, and other accomplishments. Given this variety, it should be clear that the ways of teaching and learning cannot be the same in all its branches.
One of the fundamental differences between them is that certain things that should be learned do not have a logical derivation, whereas others can be generated by a thinking individual.
If, for example, you want to get a driving license in continental Europe, you have to learn that one has to drive on the right side of the road. “Why not ride on the left?” would be a pointless question, because you have to conform to a social convention for which there is no further explanation.
In contrast, the fact that the numbers two and two yield four when they are added, can be worked out and checked by everyone who has learned to count. It does require knowledge of the conventional number-words, but from then on it is a question of conceiving units and mentally operating with them.
With this second kind of knowledge, which in principle learners can gain from their own mental operations, I want to deal later. At the moment I want to emphasize that the learning of anything that is considered ‘correct’ only because society has agreed that it should be so, is essentially a political matter.
I say ‘political’, because it concerns knowledge that the older generation wants to instill into the younger in order to assure the continuation of its society and, in an important sense, its status quo. In some respects it is quite sensible to accept this kind of knowledge. Thus, to return to the banal example of the traffic rule, it is perfectly reasonable for everyone to agree to drive on the same side of the road, but the choice of the right rather than the left does not involve rational thought.
From my point of view, it is indispensable that teachers be aware of this difference in all the matters that are to be taught, because the difference entails different teaching procedures. Whatever is conventional must be learned, so to speak, verbatim; what is based on rational operations, should be understood.
Dates in history, the names of chemical elements, the sequence of months, days of the week, number-words, and a host of other things must be learned by heart, because no amount of thought could discover them. This is to say that students must be trained so that they permanently possess these facts and are able to repeat them flawlessly whenever they are needed.
Our schools have centuries of experience with methods that are apt to bring about this kind of learning more or less successfully. It is indeed the form of learning that is generally preferred. It is preferred, for the simple reason that its results are easy to test. When students can repeat something verbatim, it is obvious that they have learned it. – Whether they have understood it, is a question these tests avoid. Educationalists do not often say this very clearly. But occasionally they do assert that the deeper purpose of school is to foster independent thinking. And this invokes the second sort of learning. I would call it conceptual learning, for it literally has to do with the activity of conceiving. To make my position as clear as possible, I am going to breach academic conventions and talk a little about my own development.
Conceptual Problems
I became aware of conceptual difficulties very early in my life, because I had the good fortune of growing up with more than one language. Here in Switzerland you have the same wonderful opportunity. Many of you will almost every day come into situations where you have to compensate for conceptual differences between French, German, and Italian. Whether you actually become aware of what the differences are, is another question. Let me give you as example a conceptual difference between French and English. In the last section of La construction du réel chez l’enfant, Piaget wrote:
L’intelligence ne débute ni par la connaissance du moi ni par celle des choses comme telles, mais par celle de leur interaction, et c’est en s’orientant simultanément vers les deux pôles de cette interaction qu’elle organise le monde en s’organisant elle-même. (Piaget, 1937, p.311)
In Margaret Cook’s English translation, the last line reads:
“intelligence organizes the world by organizing itself.” (Piaget, 1954, p.400)
I had been teaching Genetic Epistemology for quite some time at an American university where I had to use English texts, before it dawned on me that this translation was unsatisfactory. The English word ‘intelligence’ does not designate an active agent that can orient itself or organize things. To use it in this sense, is at best metaphorical. The word needed to convey what Piaget intended is ‘mind’. ‘Mind’ refers to the seat of the activities that can be called intelligent – and it is a strange fact that French, just like German, has no specific word for this. You have it as an adjective, as in ‘opérations mentales’ – to which I shall turn in a moment – but you do not have it as a specific substantive that indicates an active agent.
This is a conceptual difference, and like the thousands of others one can find, it shows that the conceptual structures underlying different languages are rarely quite the same. Many of the discrepancies are so subtle that you have to live for years in the second language before you become aware of them.
Some of you may be shocked, if I now say that you do not have to look at a foreign language to find such conceptual differences. They frequently impede mutual understanding among people who speak the same language. This should not surprise anyone who has taken to heart Ferdinand de Saussure’s fundamental insight that words do not refer to things of a real world, but to concepts in the heads of those who use language. And if you consider Piaget’s extensive analyses of how concepts are built up by means of empirical and reflective abstractions that each child has to make for itself, it becomes clear that it would be something of a miracle if the conceptual structures in different heads would be exactly the same.
The moment we get involved in a discussion of abstract items, let alone philosophical problems, we have plenty of opportunities to see how difficult mutual understanding becomes. The meanings the other attributes to the words we use are very often not quite the meanings we have in mind ourselves. Yet many people still cling to the tacit assumption that words refer to things, conditions, and events that are fundamentally unquestionable because they exist in a world that is independent of any experiencer.
This belief inevitably leads to the view that the problem of knowledge – and consequently the problem of learning – is a problem of correct description and representation of the way things are. To understand how things work, consequently, we should only have to look more closely. The age of media in which we are living today does much to perpetuate the realist belief. Radio and television programs that popularize science spread the idea that the riddles of the universe are being solved one after the other, and many popular books confirm the notion that an absolute reality is knowable and understandable. The fact that the leading scientists of the last century have all in one way or another declared that they consider their explanatory theories as hypothetical models is mostly suppressed – not only in the media, but unfortunately also in schools and institutions of higher learning, where students are to be introduced into the various scientific disciplines and scientific thinking in general.
Knowledge and a Theory of Knowing
This seems to me a good reason to take a brief look at the history of epistemology. There were single thinkers who already at the beginning of Western philosophy suspected that realism and its claim of objective knowledge were untenable. The sceptics have persistently denied such a possibility for more than two millennia. Most philosophers acknowledged the incontrovertibility of the sceptics’ arguments, but nevertheless went on hoping to find a path that would lead towards unquestionable truth about a real world. The paths they chose always led into the realms of metaphysics, that is to say, they tacitly implied some form of mystical belief.
Plato’s famous metaphor of the cave is a good example. In this fairy tale, human beings are chained in a cave the entrance to which they cannot see. In front of them, on the wall of the cave, they see shadows, and from these shadows they must guess what things there are in the world outside and what goes on there. But plato added that God, had instilled latent truths into the souls of humans, and if they learned to use their intuition, they would come to acquire truths about the real world.
This metaphor is powerful because it presents a poetically plausible situation, without making it clear that this situation could be described only by a god, for only a god could know what lies beyond the domain of human experience.
The Italian philosopher Giambattista Vico said this very nicely at the beginning of the 18th century: “God knows the world, because He created it, human beings can know only what they themselves have made.” The treatise from which this statement is taken, is the first constructivist manifesto. Immanuel Kant, some seventy years later, wrote in the Introduction to his famous Critique of pure reason: “Human reason can grasp only what she herself has produced according to her own design” (Kant, 1787).
Neither Vico nor Kant, however, was able to shake the general belief that somehow we must be able to discover how the real world really is. In my view, the persistence of this belief springs from the fact that we all have a lot of knowledge that we consider reliable, knowledge that we trust when we make decisions about how to act.
When we run down the stairs, we feel confident that the next steps will be there where we need them. And we have no less faith in much larger contexts. When I stepped into the plane to come here, I had no serious doubts that it would bring me to Geneva and that the old city would still be the one I know from many previous visits. Such faith in the permanence of objects and circumstances is essential in our everyday living – in spite of the fact that things do not always turn out quite as we expected.
We simply have to believe that, by and large, the world we experience is a stable world. But this belief should not lead us to assume that the world we experience must be like a reality that lies beyond.
The Construction of Concepts
As I said before, the great scientists of the last century became aware of this impasse. Physicists, to take them as prototype, must of course assume that the world they experience and experimentally observe has stability. But this assumption, no matter how well it works, does not justify the conclusion that their explanations can explain a reality as it might be independently of the observer.
This agnostic position can be justified by all sorts of epistemological considerations. But as I want to focus on concepts, I shall quote something Albert Einstein wrote exactly fifty years ago:
Physical concepts are free creations of the human mind, and are not, however it may seem, uniquely determined by the external world. (Einstein & Infeld, 1950)
From the constructivist point of view, creating concepts is a form of construction – and construction, under all circumstances, involves reflection. In this context, reflection means to become aware of connections that it is possible to make by coordinating sensory elements or mental operations. Piaget generally speaks of “coordination”. And this, obviously, is done by a MIND. Many of these coordinations quickly turn into habits and are then carried out without conscious awareness.
Because mental operations necessarily take place in someone’s head, they cannot be depicted. But I can reproduce a picture here, that will show that it is you yourselves who produce your specific perception.
To most viewers, this picture will seem meaningless at first. But the moment it is turned round, you recognize something familiar. You will probably say: “It’s a dog!”
In fact, it is nothing but a collection of irregular black splotches. Thus the question is: Where is the dog?
In case someone still thinks that the dog must be somehow on the sheet of paper, I will show you another example.
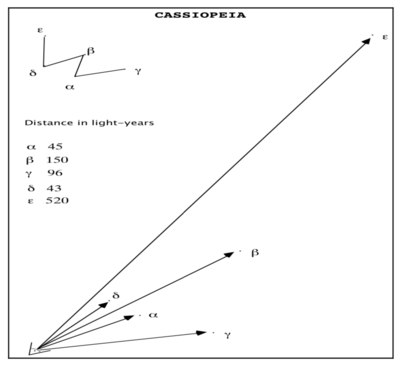
I suppose you are familiar with the constellation that is called Cassiopeia. It’s a big, capital double-U or, if you turn it round, an M. You can see it near the Polar Star, opposite the Big Bear. The Greeks called it the Crown of Cassiopeia, and it has survived the three thousand years since then without noticeable change. It’s as permanent and durable as one might wish. Yet, again, I would like to ask you: Where is it? – “It’s in the sky, of course”, you might say.
Like President Clinton, speaking about his unsavory amorous exploits, I want to question the meaning of “is”. The constellation consists of five stars that astronomers designate by Greek letters.
Alpha and Delta are about 40 light years from the Earth. Gamma is twice as far, Beta, three times as far – and the distance to Epsilon is 520 light years, which means it is more than ten times as far from Earth as the first two stars.
Imagine now that you are traveling in a space ship in the direction towards Epsilon. What happens? After a few light years, the double-U that you saw from Earth has spread so much that you have difficulty in connecting the five stars. After a tenth of the journey, Alpha and Delta lie behind you. The constellation, whose existence you confidently relied on when you sailed your boat at night, has disintegrated.
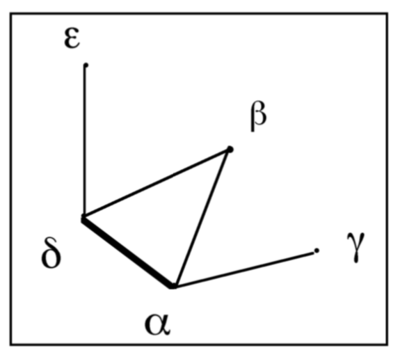
Seeing the double-U depends on two things:
1) a specific point of observation;
2) carrying out specific perceptual operations.
Piaget always maintained that perception was a form of action. Silvio Ceccato suggested that it is the movements of attention that generate the form and shapes we perceive (Ceccato, 1974, p.231). Attention, he said, is not like a spotlight that illuminates objects, but it is a pulse that focuses on sensory differences; and by moving from one point to another it produces outlines. Thus, once you have picked stars out of the darkness of the sky, your focus of attention connects them by moving from one to the other.
With the five stars of the Cassiopeia, there are several possibilities. Here are two:
These patterns are not produced, because of the general tendency to look for something familiar, which is to say, the tendency to assimilate. As in the case of the dog, you ternd to see what you have seen before. And in today’s Western world the capital double-U is surely the most familiar pattern for five such points. The Greeks had no double-U, but regularly crowned heros, kings, and queens; so they perceived the five stars as a crown.
You may be inclined to think that these are merely optical tricks and the important concepts that teachers are concerned with, are not just images in people’s heads. Let me therefore explain a very important concept and how I think it may be constructed.
The Concept of Plurality
How does a child come to use the plural form of words correctly?
Imagine a two-year-old girl who a little while ago learned to say the word “apple”
when it encounters a round, more or less red object that it can bite into and that sometimes tastes quite good. She now comes into the kitchen, and there are several apples lying on the table. With a certain amount of pride she points at one, and says “apple”. Then she points at the second one, and says “apple”. Maybe she repeats this with all of them.
“Yes, my dear,” says the mother, “they are apples.”
Perhaps the little girl notices the difference in the word the first time. In any case, she will hear the plural form of the word in other settings – and lo and behold, it does not take long before she uses singular and plural just as the linguistic convention demands it.
How does the child learn it? All the apples she sees correspond to a kind of ‘recognition matrix’. This matrix is what Piaget called an empirical abstraction – and it is the one with which she has associated the word ‘apple’. But none of those individual apples can tell her that it belongs to a plurality which the adults call ‘apples’. The difference literally has to be conceived. It is not a matter of visual perception; it can be made only by a reflection on one’s own operating.
Apparently, this was deemed so obvious that, as far as I know, no writer on developmental psychology has mentioned it. Yet, this does not mean that it was properly understood.
The concept of plurality requires at least the following operations. Having recognized an object as, for instance, an ‘apple’, attention has to be focused immediately on at least one other object that fits the same recognition matrix. The salient point is that one and the same recognition matrix can be applied successfully more than once within the context. This repetition does not reside in the objects. Each of the apples in the example lies on the table and gives no indication that there are others. The repetition can spring only from something the perceiver does. This is to say, in order to apply the plural correctly, the little girl must in some way become aware of her own operations of recognition.
Ceccato coined the expression ‘consapevolezza operativa’. It stands for ‘operational awareness’ and is, I think, in many ways similar to what Piaget, somewhat less transparently, called “thematization”.
I have used the example of the plural many times, because it is the simplest and clearest that I know. Concepts such as ‘beginning’ and ‘end’, ‘duration’ and ‘change’, ‘space’ and ‘time’, and in my view all abstract concepts, can be explained in this fashion. True, they require different and sometimes highly complex mental operations, but it is always the experiencer’s attention on his or her own operating that brings them forth.
If you find this analysis appropriate, you may agree with my claim that it has a variety of consequences for teaching. As soon as it is clear that students must build their concepts by their own reflections, the notion that concepts can be conveyed by means of language is no longer tenable. As I tried to show at the beginning of my talk, the words that someone utters are interpreted by others in terms of the concepts these others already have. Only if their first spontaneous interpretation does not seem to make sense, will they be likely to attempt a new conceptualization.
My friend Humberto Maturana has suggested that language has the function of orienting. I consider this an important insight. Consequently, I have no illusion that my exposition here could give you a new conceptual network. I would be happy if I succeeded in evoking a doubt here and there – a doubt that might lead you to some novel constructions.
An Example of Active Learning
This brings me to a point which, I believe, is indispensable for didactics. There is no infallible method of teaching conceptual thinking. But one of the most successful consists in presenting students with situations in which their habitual thinking fails. I shall lay out an example of this method that was developed by Leonard and Gerace at our institute at the University of Massachusetts.
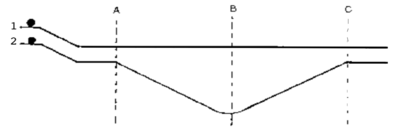
Here you have a schematic representation of an apparatus that reminds me of a game that we passionately played as children, if there was a big heap of sand or at the beach. We made a kind of bobsleigh track, and let our large glass marbles roll down to see which was the fastest.
What you see here, are two tracks on which steel balls can roll with almost no frictional loss of energy. The two tracks are not the same, but start and finish are on the same height for both. The question is, which of the two balls will reach the finish first, if they are started at the same time?
Many of the beginning physics students to whom the question is put, say that number 1 will arrive first, because number 2 has a longer path.
Others predict that the balls will arrive simultaneously, because, although number 2 gains a lead on the downhill slope, it will lose it when it has to roll uphill.
Very rarely one answers that number 2 will win the race.
Hence there is considerable surprise when the balls are actually let roll, and number 2 arrives first every time. Some of the students laugh and say that we have somehow managed to build a trick into the display.
We assure them that there is no trick, and ask them to describe, as accurately as they can, what happens on each of the sections of the track. At first it is often not easy to get them to talk. But when we assure them that this is not a test and that we merely want them to share with the others what they are thinking, one or two begin, and then others join in. It usually does not take long for them to agree on the following descriptions: At point A, both balls arrive at the same moment and with the same speed. The slope from A to B accelerates number 2 and it therefore reaches point B before number 1. – “Number 2 has a lead?” we ask. Yes. At point B, number 2 has a lead – but then it has to roll uphill and it loses its lead. – We ask: “And when number 2 reaches point C, does it roll faster or slower than number 1? Usually this triggers a longer discussion, but eventually the students agree that the negative acceleration on the uphill section equals the positive acceleration on the downhill and therefore the two balls should have the same speed at point C. This is the moment when some catch a glimpse of the insight that number 2 rolls faster than number 1 over the entire stretch from A to C. The lead it gains does more than cover the longer path, and therefore it arrives first at the finish. Of course, not all the students are immediately convinced. But those who have seen the solution are usually indefatigable in explaining it to others. In the end, most of them understand how, as physicists, they have to conceptualize the situation.
Suggestions for Teachers
I consider this an ideal example of teaching and learning. The teacher presents a situation in which the students’ network of explanatory concepts clearly turns out to be unsatisfactory. Nothing is condemned as “wrong”, and no “correct” explanations are provided by the teacher. The students’ thinking is merely oriented now and then by neutral questions.
The main principles of constructivist didactics are implicit in this example. They are simple, but I want to emphasize some of them.
1 – Teaching does not begin with the presentation of sacred truths, but with creating opportunities to trigger the students’ own thinking. One of the prerequisites for this would be that the teacher believes that students can think. In our schools in the United States, this belief is by no means universally manifest.
2 – It is not sufficient for teachers to be familiar with the subject matter of the curriculum; they also have to have a repertoire of didactic situations in which the concepts that are to be built up can be involved. And these situations should be such that they evoke the students’ spontaneous interest. Both these requirements are often disregarded. The fundamental fact that concepts can be formed only in the experiential world of an individual remains buried under the general notion that everything conceptual is but a representation of an independent reality and can therefore be transferred to students ready-made. But this kind of realism is a poor basis for teaching.
3 – Whenever students show their work, it is misguided for the teacher to say that it is ‘wrong’ – irrespective of how justified this judgement might be. Students rarely produce a random solution. They have worked at it, and if the result which they consider to be right at the moment is not what the teacher thinks it should be, their effort must nevertheless be acknowledged. Disregarding it, is a sure way to demolish whatever spark of motivation they had. And then it is not surprising that their willingness to tackle new tasks disappears. I began my talk dwelling on the relativity of word meanings and this is a point I want to return to once more in the context of teaching.
4 – Many words that teachers habitually associate with specialized meanings in the particular discipline, evoke very different associations in the beginning student. An understanding of the desired conceptual network (especially in scientific domains) becomes possible only when ‘naive’ concepts are consciously reconstructed. In order to foster such reconstruction and the formation of new conceptual relations, teachers must have at least an inkling of the students’ present ideas and theories. Only if they have some model of the students’ thinking, can they begin to orient trains of thought and try to preclude ‘inappropriate’ constructions.
5 – If it is the case that the formation of concepts requires reflection, teachers must have available some means to provoke it. By far the easiest way is to get students to talk about what they are thinking. The act of verbalization requires a review of what is to be verbalized. This review is a form of reflection and often brings to the surface inconsistencies or gaps in a train of thought. Hence it is crucial to initiate conversations whenever a problem is to be solved. It may be students explaining their thinking to the teacher or explaining it to their classmates. Both lead to reflection and are the beginning of what Ceccato called ‘operational awareness’. After a while this becomes a habit for the students, and then all problem-solving can turn into a conversation with oneself.
Conclusion
Before I close, I would like to answer the most frequent objection made by teachers to the constructivist approach. All this, they say, is very nice and even quite reasonable, but how could teachers possibly find the time to engage in procedures that deal with the thinking of individual students, when the pressure to keep up with the time table of the curriculum is already more than they can manage. My answer is simple and may sound utopian, but evidence is beginning to show that it works.
Let us assume you devote one or even two whole lessons to an experiment like that of the marble tracks I have shown. This was done at our institute, and the experience left no doubt that it led students to learn far more than just the explanation of a surprising result. They began to realize that conscious reflection is the secret of understanding.
Where the teaching of physics is concerned, I might add that the experiment I have described also offers the possibility in subsequent lessons to deal with concepts such as velocity, inertia, gravitation, friction, and air resistance – and it can now be done by referring to an experience the students have actually had.
If you provide them with one or two further opoortunities of this kind, the realization gets confirmed and they will have learned to think. From then on, they will be able to tackle all sorts of new problems productively and they will have gained some of the confidence that is the prerequisite of motivation. Moreover, their new insight is not confined to physics. It is applicable to learning in general, will be helpful in all disciplines, and is bound to accelerate their progress.
If the teachers in other disciplines provide similar occasions for students’ autonomous construction and testing of concepts, they will be amazed how much easier it becomes to have students actually understand and thus truly cover the required subject matter.
Of course, I do not expect that you believe me – but I hope you will experiment with some of the suggestions I have made, for then you will see for yourselves that they work.
References
Ceccato, S. (1974) La terza cibernetica. Milan: Feltrinelli.
Einstein, A. & Infeld, L. (1950), Die Evolution der Physik. Wien: Paul Zsolnay.
Kant, I. (1787) Kritik der reinen Vernunft (Critique of pure reason; 2nd edition). Berlin: Akademieausgabe, Vol.III.
Leonard, W.J., & Gerace, W. (1996) The power of simple reasoning, Physics Teacher, 34, 280-283.
Piaget, J. (1936) La construction du réel chez l’enfant. Neuchâtel: Delachaux et Niestlé.
Piaget, J. (1954) The construction of reality in the child. Translation by M.Cook. New York: Ballantine.
Vernon, M.D. (1947) Different types of perceptual ability, British Journal of Psychology, 38, 79.